
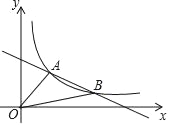
【题目】如图,一次函数y1=﹣![]() x+4的图象与反比例函数y2=
x+4的图象与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点
的图象交于A(2,3),B(6,n)两点
(1)观察图象当y1>y2时,x的取值范围是 ;
(2)求反比例函数的解析式及B点坐标;
(3)求△OAB的面积.
【答案】(1)x<0或2<x<6;(2)y2=![]() ,(6,1);(3)8.
,(6,1);(3)8.
【解析】
(1)观察函数图象得到当x<0或2<x<6时,一次函数图象在反比例函数图象的上方;
(2)把A(2,3)代入y2=![]() ,利用待定系数法求反比例函数的解析式;将B(6,n)代入y1=﹣
,利用待定系数法求反比例函数的解析式;将B(6,n)代入y1=﹣![]() x+4可求出n的值,即可求出B点坐标;
x+4可求出n的值,即可求出B点坐标;
(3)求得直线与x轴的交点坐标,根据三角形面积公式即可求得.
解:(1)根据图象可知,当y1>y2时,x的取值范围是x<0或2<x<6.
故答案为x<0或2<x<6;

(2)把A(2,3)代入y2=![]() ,得m=2×3=6,
,得m=2×3=6,
∴反比例函数的解析式为y2=![]() ;
;
将B(6,n)代入y1=﹣![]() x+4,
x+4,
得n=﹣![]() ×6+4=1,
×6+4=1,
∴B点坐标为(6,1);
(3)由直线y1=﹣![]() x+4可知与x轴的交点为(8, 0),
x+4可知与x轴的交点为(8, 0),
又∵A(2,3),B(6,1),
∴S△AOB=![]() ×8×3﹣
×8×3﹣![]() ×8×1=8.
×8×1=8.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,线段EF在对角线AC上(E不与A重合,F不与C重合),EG⊥AD,FH⊥BC,垂足分别是G、H,且EG+FH=EF.
(1)写出图中与△AEG相似的三角形;
(2)求线段EF的长;
(3)设EG=x,△AEG与△CFH的面积和为S,写出S关于x的函数关系式及自变量x的取值范围,并求出S的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c的图象过点A(3,0),C(﹣1,0).
(1)求二次函数的解析式;
(2)如图,点P是二次函数图象的对称轴上的一个动点,二次函数的图象与y轴交于点B,当PB+PC最小时,求点P的坐标;
(3)在第一象限内的抛物线上有一点Q,当△QAB的面积最大时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF![]() DE.
DE.
(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若 AD![]() 4,DE
4,DE![]() 5,求DM的长.
5,求DM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在把一张正方形纸片按如图方式剪去一个半径为40![]() 厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,
厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

A. 64 B. 67 C. 70 D. 73
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁,
(I)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A'C'的位置时,A'C'的长为 .
(II)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°。已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com