
【题目】如图,在ABCD中,E为边AD上的一点,将△DEC沿CE折叠至△D′EC处,若∠B=48°,∠ECD=25°,则∠D′EA的度数为( )

A.33°B.34°C.35°D.36°
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为![]() ,则取出了多少个黑球?
,则取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
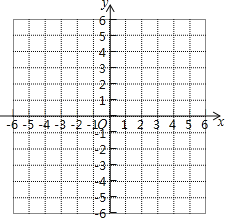
【题目】如图是一个平面直角坐标系.
(1)请在图中描出以下6个点:A(0,2)、B(4,2)、C(3,4)A′(-4,-4)、B'(0,-4)、C′(-1,-2)
(2)分别顺次连接A、B、C和A′、B'、C',得到三角形ABC和三角形A′B′C′;
(3)观察所画的图形,判断三角形A′B′C′能否由三角形ABC平移得到,如果能,请说出三角形A′B′C′是由三角形ABC怎样平移得到的;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,三角形OAB的边OA、OB分别在x轴正半轴上和y轴正半轴上,A(a,0),a是方程![]() 的解,且△OAB的面积为6.
的解,且△OAB的面积为6.
(1)求点A、B的坐标;
(2)将线段OA沿轴向上平移后得到PQ,点O、A的对应点分别为点P和点Q(点P与点B不重合),设点P的纵坐标为t,△BPQ的面积为S,请用含t的式子表示S;
(3)在(2)的条件下,设PQ交线段AB于点K,若PK=![]() ,求t的值及△BPQ的面积.
,求t的值及△BPQ的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:材料1:符号“ ”称为二阶行列式,规定它的运算法则为
”称为二阶行列式,规定它的运算法则为 .如
.如![]() .
.
材料2:我们已经学习过求解一元一次方程、二元一次方程组、分式方程等方程的解法,虽然各类方程的解法不尽相同,但是蕴含了相同的基本数学思想——转化,把未知转化为已知.用“转化”的数学思想,还可以解一些新的方程.例如,求解部分一元二次方程![]() 时,我们可以利用因式分解把它转化为一元一次方程来求解.如解方程:
时,我们可以利用因式分解把它转化为一元一次方程来求解.如解方程:![]() .∵
.∵![]() ∴
∴![]() .故
.故![]() 或
或![]() .因此原方程的解是
.因此原方程的解是![]() ,
,![]() .
.
根据材料回答以下问题:
(1)二阶行列式![]() ___________;二阶行列式
___________;二阶行列式![]() 中
中![]() 的值为__________.
的值为__________.
(2)求解![]() 中
中![]() 的值.
的值.
(3)结合材料,若![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在"元旦"期间,几名学生随同家长一起到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)小明他们一共去了几名成人,几名学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
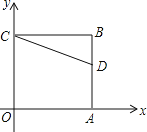
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com