
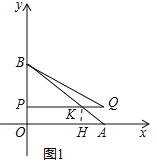
【题目】如图,在平面直角坐标系中,点O为坐标原点,三角形OAB的边OA、OB分别在x轴正半轴上和y轴正半轴上,A(a,0),a是方程![]() 的解,且△OAB的面积为6.
的解,且△OAB的面积为6.
(1)求点A、B的坐标;
(2)将线段OA沿轴向上平移后得到PQ,点O、A的对应点分别为点P和点Q(点P与点B不重合),设点P的纵坐标为t,△BPQ的面积为S,请用含t的式子表示S;
(3)在(2)的条件下,设PQ交线段AB于点K,若PK=![]() ,求t的值及△BPQ的面积.
,求t的值及△BPQ的面积.

【答案】(1)B(0,3);(2)S=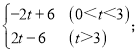 (3)4
(3)4
【解析】
(1)解方程求出a的值,利用三角形的面积公式构建方程求出b的值即可解决问题;
(2)分两种情形分别求解:当点P在线段OB上时,当点P在线段OB的延长线上时;
(3)过点K作KH⊥OA用H.根据S△BPK+S△AKH=S△AOB-S长方形OPKH,构建方程求出t,即可解决问题;
解:(1)∵![]() ,
,
∴2(a+2)-3(a-2)=6,
∴-a+4=0,
∴a=4,
∴A(4,0),
∵S△OAB=6,
∴![]() 4OB=6,
4OB=6,
∴OB=3,
∴B(0,3).
(2)当点P在线段OB上时,S=![]() PQPB=
PQPB=![]() ×4×(3-t)=-2t+6.
×4×(3-t)=-2t+6.
当点P在线段OB的延长线上时,S=![]() PQPB=
PQPB=![]() ×4×(t-3)=2t-6.
×4×(t-3)=2t-6.
综上所述,S=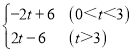 .
.
(3)过点K作KH⊥OA用H.
∵S△BPK+S△AKH=S△AOB-S长方形OPKH,
∴![]() PKBP+
PKBP+![]() AHKH=6-PKOP,
AHKH=6-PKOP,
∴![]() ×
×![]() ×(3-t)+
×(3-t)+![]() (4-
(4-![]() )t=6-
)t=6-![]() t,
t,
解得t=1,
∴S△BPQ=-2t+6=4.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
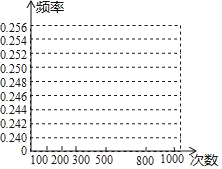
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
(1)填空:a= ,b= ;
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
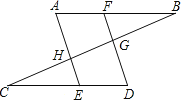
【题目】已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.
(1)求证:AB∥CD;
(2)若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边AD上的一点,将△DEC沿CE折叠至△D′EC处,若∠B=48°,∠ECD=25°,则∠D′EA的度数为( )

A.33°B.34°C.35°D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
![]() ;
;
![]() ;
;
![]() ;
;
……
(1)根据以上规律,可知![]() __________;
__________;
(2)你能否由此归纳出一般性规律:![]() __________;
__________;
(3)根据(2)求出:![]() .的个位数字是几?
.的个位数字是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx﹣3(b是常数)经过点A(﹣1,0).
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.
① 当点P' 落在该抛物线上时,求m的值;
② 当点P' 落在第二象限内,P'A2取得最小值时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com