
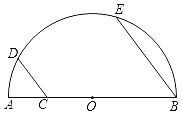
【题目】如图:AB为半圆的直径,AB=4,C为OA中点,D为半圆上一点,连CD,E为![]() 的中点,且CD∥BE,则CD的长为( )
的中点,且CD∥BE,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,由题意,可得△BHE≌△DHK,所以BE=KD=2x,EH=KH,由△KCO∽△EBO,可得![]() ,所以KO=1,KC=x,在Rt△BHE和Rt△BHO中,有BE2﹣EH2=BH2=BO2﹣OH2,即可得出x的值,进而得出CD的长.
,所以KO=1,KC=x,在Rt△BHE和Rt△BHO中,有BE2﹣EH2=BH2=BO2﹣OH2,即可得出x的值,进而得出CD的长.
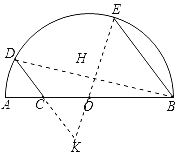
解:如图,连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,
∵E为弧AD中点,
∴OE⊥AD,BH=DH,
∵BE∥CD,
∴∠EBH=∠KDH,∠E=∠K,
∴△BHE≌△DHK(AAS),
∴BE=KD=2x,EH=KH,
∵BE∥CD,
∴△KCO∽△EBO,
∴![]() ,
,
∵AB是半圆⊙O的直径,AB=4,C为OA的中点,
∴![]() ,
,
∴KO=1,KC=x,
∴KE=KO+OE=1+2=3,
∴EH=KH=1.5,OH=0.5,
∵BE2﹣EH2=BH2=BO2﹣OH2,
∴4x2﹣1.52=22﹣0.52,
解得:x![]() ,
,
∴CD=KD﹣KC=2x﹣x=x![]() ,
,
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,AB=AC,边BC长为6,高AD长为4,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,则正方形PQMN的边长为( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
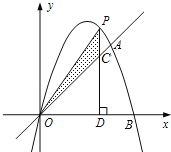
【题目】如图,已知抛物线y=ax2+bx+c的图象经过点A(3,3)、B(4,0)和原点O,P为直线OA上方抛物线上的一个动点.
(1)求直线OA及抛物线的解析式;
(2)过点P作x轴的垂线,垂足为D,并与直线OA交于点C,当△PCO为等腰三角形时,求D的坐标;
(3)设P关于对称轴的点为Q,抛物线的顶点为M,探索是否存在一点P,使得△PQM的面积为![]() ,如果存在,求出P的坐标;如果不存在,请说明理由.
,如果存在,求出P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
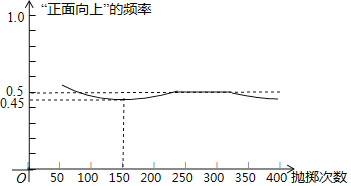
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批康乃馨,经分析上一年的销售情况,发现这种康乃馨每天的销售量y(支)是销售单价x(元)的一次函数,已知销售单价为7元/支时,销售量为16支;销售单价为8元/支时,销售量为14支.
(1)求这种康乃馨每天的销售量y(支)关于销售单价x(元/支)的一次函数解析式;
(2)若按去年方式销售,已知今年这种康乃馨的进价是每支5元,商家若想每天获得42元的利润,销售单价要定为多少元?
(3)在(2)的条件下,当销售单价x为何值时,花店销售这种康乃馨每天获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,E,F在BC、CD上,以EF为直径的半圆切AD于G(如图1).
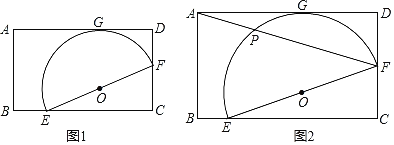
(1)求证:CE=2DG;
(2)若F为DC中点,连AF交半圆于P(如图2),且AB=4,AD=5![]() ,求PF.
,求PF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)

(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com