
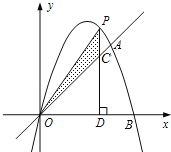
【题目】如图,已知抛物线y=ax2+bx+c的图象经过点A(3,3)、B(4,0)和原点O,P为直线OA上方抛物线上的一个动点.
(1)求直线OA及抛物线的解析式;
(2)过点P作x轴的垂线,垂足为D,并与直线OA交于点C,当△PCO为等腰三角形时,求D的坐标;
(3)设P关于对称轴的点为Q,抛物线的顶点为M,探索是否存在一点P,使得△PQM的面积为![]() ,如果存在,求出P的坐标;如果不存在,请说明理由.
,如果存在,求出P的坐标;如果不存在,请说明理由.
【答案】(1)直线OA的解析式为y=x,二次函数的解析式是y=﹣x2+4x;(2)D(![]() );(3)存在,P(
);(3)存在,P(![]() )或(
)或(![]() ).
).
【解析】
(1)设直线OA的解析式为y1=kx,把点A坐标(3,3)代入得:k=1,直线OA的解析式为y=x;再设y2=ax(x4),把点A坐标(3,3)代入得:a=1,即可求解;
(2)P为直线OA上方抛物线上的一个动点,故0<m<3.此时仅有OC=PC,CO=![]() OD=
OD=![]() m,
m,![]() ,解得
,解得![]() ,即可求解;
,即可求解;
(3)M到直线PQ的距离为4(n2+4n)=(n2)2,要使△PQM的面积为![]() ,则
,则![]() ,即
,即![]() ,即可求解.
,即可求解.
解:(1)设直线OA的解析式为y1=kx,
把点A坐标(3,3)代入得:k=1,
直线OA的解析式为y=x;
再设y2=ax(x﹣4),
把点A坐标(3,3)代入得:a=﹣1,
函数的解析式为y=﹣x2+4x,
∴直线OA的解析式为y=x,二次函数的解析式是y=﹣x2+4x.
(2)设D的横坐标为m,则P的坐标为(m,﹣m2+4m),
∵P为直线OA上方抛物线上的一个动点,
∴0<m<3.
此时仅有OC=PC,CO=![]() =
=![]() OD=
OD=![]() m,
m,
∴![]() ,解得
,解得![]() ,
,
∴![]() ;
;
(3)函数的解析式为y=﹣x2+4x,
∴对称轴为x=2,顶点M(2,4),
设P(n,﹣n2+4n),则点P关于对称轴的对称点Q(4﹣n,﹣n2+4n),
M到直线PQ的距离为4﹣(﹣n2+4n)=(n﹣2)2,
要使△PQM的面积为![]() ,
,
则![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ,
,
∴P(![]() )或(
)或(![]() ).
).


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
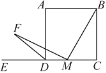
【题目】如图,在正方形ABCD中,AB=2,点M为正方形ABCD的边CD上的动点(与点C,D不重合),连接BM,作MF⊥BM,与正方形ABCD的外角∠ADE的平分线交于点F.设CM=x,△DFM的面积为y,则y与x之间的函数关系式为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东30°方向,距离灯塔100海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.

(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔150海里的点O处.圆形暗礁区域的半径为60海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险?如果海轮从B处继续向正北方向航行,是否有触礁的危险?并说明理由.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
(1)求证:FG=FB.
(2)若tan∠F=![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
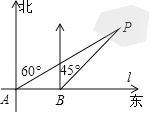
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5秒时,PD的长是( )
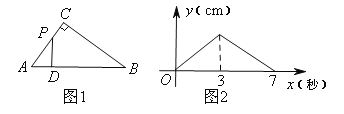
A.1.5cmB.1.2cmC.1.8cmD.2cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com