
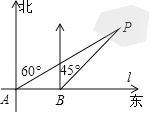
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
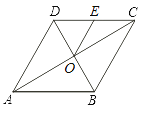
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
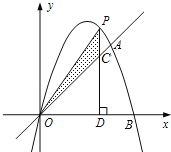
【题目】如图,已知抛物线y=ax2+bx+c的图象经过点A(3,3)、B(4,0)和原点O,P为直线OA上方抛物线上的一个动点.
(1)求直线OA及抛物线的解析式;
(2)过点P作x轴的垂线,垂足为D,并与直线OA交于点C,当△PCO为等腰三角形时,求D的坐标;
(3)设P关于对称轴的点为Q,抛物线的顶点为M,探索是否存在一点P,使得△PQM的面积为![]() ,如果存在,求出P的坐标;如果不存在,请说明理由.
,如果存在,求出P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴分别交于A(﹣3,0),B两点,与y轴交于点C,抛物线的顶点E(﹣1,4),对称轴交x轴于点F.
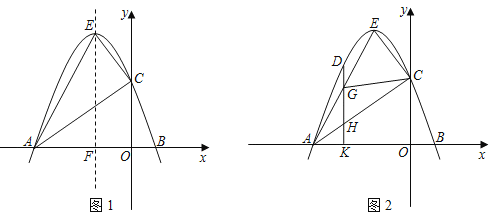
(1)请直接写出这条抛物线和直线AE、直线AC的解析式;
(2)连接AC、AE、CE,判断△ACE的形状,并说明理由;
(3)如图2,点D是抛物线上一动点,它的横坐标为m,且﹣3<m<﹣1,过点D作DK⊥x轴于点K,DK分别交线段AE、AC于点G、H.在点D的运动过程中,
①DG、GH、HK这三条线段能否相等?若相等,请求出点D的坐标;若不相等,请说明理由;
②在①的条件下,判断CG与AE的数量关系,并直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
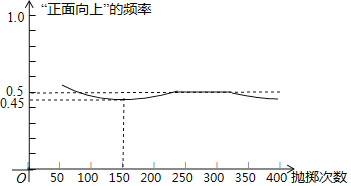
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批康乃馨,经分析上一年的销售情况,发现这种康乃馨每天的销售量y(支)是销售单价x(元)的一次函数,已知销售单价为7元/支时,销售量为16支;销售单价为8元/支时,销售量为14支.
(1)求这种康乃馨每天的销售量y(支)关于销售单价x(元/支)的一次函数解析式;
(2)若按去年方式销售,已知今年这种康乃馨的进价是每支5元,商家若想每天获得42元的利润,销售单价要定为多少元?
(3)在(2)的条件下,当销售单价x为何值时,花店销售这种康乃馨每天获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为正整数的正方形ABCD被分成了四个小长方形且点E,F,G,H在同一直线上(点F在线段EG上),点E,N,H,M在正方形ABCD的边上,长方形AEFM,GNCH的周长分别为6和10.则正方形ABCD的边长的最小值为( )
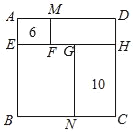
A.3B.4C.5D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com