
【题目】如图,边长为正整数的正方形ABCD被分成了四个小长方形且点E,F,G,H在同一直线上(点F在线段EG上),点E,N,H,M在正方形ABCD的边上,长方形AEFM,GNCH的周长分别为6和10.则正方形ABCD的边长的最小值为( )
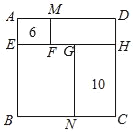
A.3B.4C.5D.不能确定
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
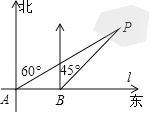
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
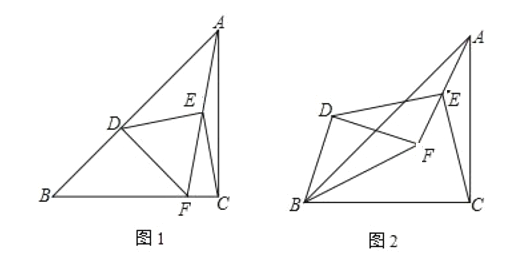
【题目】已知如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于
于![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)写出线段![]() 与线段
与线段![]() 的关系并证明;
的关系并证明;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,其它条件不变,线段
,其它条件不变,线段![]() 与线段
与线段![]() 的关系是否变化,写出你的结论并证明;
的关系是否变化,写出你的结论并证明;
(3)将![]() 绕点
绕点![]() 逆时针旋转一周,如果
逆时针旋转一周,如果![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5秒时,PD的长是( )
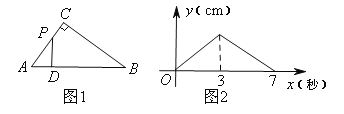
A.1.5cmB.1.2cmC.1.8cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
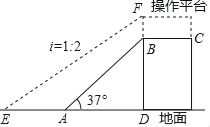
【题目】如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.
(1)求传送带AB的长度;
(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.41,
≈1.41, ![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图(1),![]() ,
,![]() ,
,![]() ,
,![]() 四点分别在四边形
四点分别在四边形![]() 的四条边上,若四边形
的四条边上,若四边形![]() 为菱形,我们称菱形
为菱形,我们称菱形![]() 为四边形
为四边形![]() 的内接菱形.
的内接菱形.
动手操作:

(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由![]() 个小正方形组成一个大正方形
个小正方形组成一个大正方形![]() ,点
,点![]() 、
、![]() 在格点上,请在图(2)中画出四边形
在格点上,请在图(2)中画出四边形![]() 的内接菱形
的内接菱形![]() ;
;
特例探索:
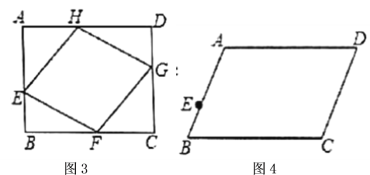
(2)如图3,矩形![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,四边形
,四边形![]() 是矩形
是矩形![]() 的内接菱形,求
的内接菱形,求![]() 的长度;
的长度;
拓展应用:
(3)如图4,平行四边形![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,
,
①请你在图4中画出平行四边形![]() 的内接菱形
的内接菱形![]() ,点
,点![]() 在边
在边![]() 上;
上;
②在①的条件下,当![]() 的长最短时,
的长最短时,![]() 的长为__________
的长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AC平分∠DAB,直线DC与AB的延长线相交于点P,AD与PC延长线垂直,垂足为D,CE平分∠ACB,交⊙O于E.
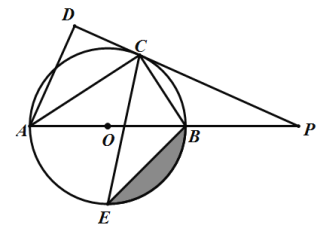
(1)求证:PC与⊙O相切;
(2)若AC=6,tan∠BEC=![]() ,求BE的长度以及图中阴影部分面积.
,求BE的长度以及图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
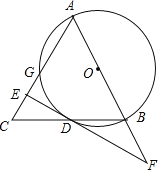
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点G,过D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)当∠BAC=60°,AB=8时,求EG的长;
(3)当AB=5,BC=6时,求tanF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
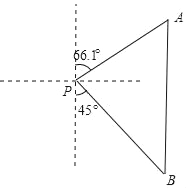
【题目】如图,一艘海轮位于灯塔P的北偏东66.1°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).
参考数据:sin66.1°≈0.91,cos66.1°≈0.41,tan64°≈2.26,![]() 取1.414.
取1.414.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com