
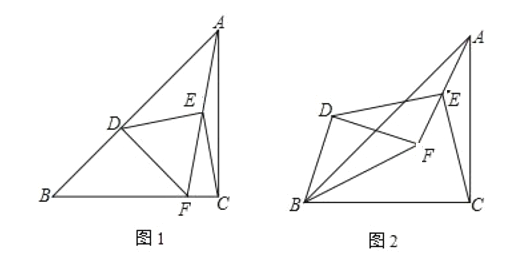
【题目】已知如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于
于![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)写出线段![]() 与线段
与线段![]() 的关系并证明;
的关系并证明;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,其它条件不变,线段
,其它条件不变,线段![]() 与线段
与线段![]() 的关系是否变化,写出你的结论并证明;
的关系是否变化,写出你的结论并证明;
(3)将![]() 绕点
绕点![]() 逆时针旋转一周,如果
逆时针旋转一周,如果![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的范围.
的范围.
【答案】(1)![]() ,
,![]() ,证明见解析;(2)结论不变,理由见解析;(3)最大值
,证明见解析;(2)结论不变,理由见解析;(3)最大值![]() 最小值
最小值![]() .
.
【解析】
(1)在Rt△ADF中,可得DE=AE=EF,在Rt△ABF中,可得BE=EF=EA,得证ED=EB;然后利用等腰三角形的性质以及四边形ADFB的内角和为180°,可推导得出∠DEB=90°;
(2)如下图,先证四边形MFBA是平行四边形,再证△DCB≌△DFM,从而推导出△DMB是等腰直角三角形,最后得出结论;
(3)如下图,当点F在AC上时,CE有最大值;当点F在AC延长线上时,CE有最小值.
(1)∵DF⊥AC,点E是AF的中点
∴DE=AE=EF,∠EDF=∠DFE
∵∠ABC=90°,点E是AF的中点
∴BE=AE=EF,∠EFB=∠EBF
∴DE=EB
∵AB=BC,
∴∠DAB=45°
∴在四边形ABFD中,∠DFB=360°-90°-45°-90°=135°
∠DEB=∠DEF+∠FEB=180°-2∠EFD+180°-2∠EFB=360°-2(∠EFD+∠EFB)
=360°-2×135°=90°
∴DE⊥EB
(2)如下图,延长BE至点M处,使得ME=EB,连接MA、ME、MF、MD、FB、DB,延长MF交CB于点H
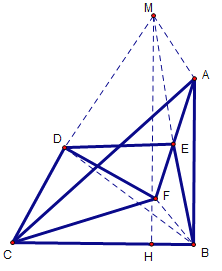
∵ME=EB,点E是AF的中点
∴四边形MFBA是平行四边形
∴MF∥AB,MF=AB
∴∠MHB=180°-∠ABC=90°
∵∠DCA=∠FCB=![]()
∴∠DCB=45°+![]() ,∠CFH=90°-
,∠CFH=90°-![]()
∵∠DCF=45°,∠CDF=90°
∴∠DFC=45°,△DCF是等腰直角三角形
∴∠DFM=180°-∠DFC-∠CFH=45°+![]()
∴∠DCB=∠DFM
∵△ABC和△CDF都是等腰直角三角形
∴DC=DF,BC=AB=MF
∴△DCB≌△DFM(SAS)
∴∠MDF=∠BDC,DB=DM
∴∠MDF+∠FDB=∠BDC+∠FDB=90°
∴△DMB是等腰直角三角形
∵点E是MB的中点
∴DE=EB,DE⊥EB
(3)当点F在AC上时,CF有最大值,图形如下:
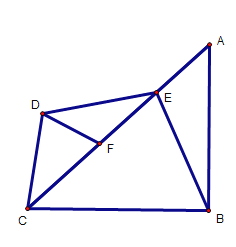
∵BC=6,∴在等腰直角△ABC中,AC=6![]()
∵CF=3![]() ,∴AF=3
,∴AF=3![]()
∴CE=CF+FE=CF+![]()
![]()
当点F在AC延长线上时,CE有最小值,图形如下:
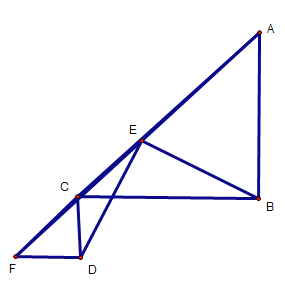
同理,CE=EF-CF![]()


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批康乃馨,经分析上一年的销售情况,发现这种康乃馨每天的销售量y(支)是销售单价x(元)的一次函数,已知销售单价为7元/支时,销售量为16支;销售单价为8元/支时,销售量为14支.
(1)求这种康乃馨每天的销售量y(支)关于销售单价x(元/支)的一次函数解析式;
(2)若按去年方式销售,已知今年这种康乃馨的进价是每支5元,商家若想每天获得42元的利润,销售单价要定为多少元?
(3)在(2)的条件下,当销售单价x为何值时,花店销售这种康乃馨每天获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)

(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
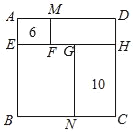
【题目】如图,边长为正整数的正方形ABCD被分成了四个小长方形且点E,F,G,H在同一直线上(点F在线段EG上),点E,N,H,M在正方形ABCD的边上,长方形AEFM,GNCH的周长分别为6和10.则正方形ABCD的边长的最小值为( )
A.3B.4C.5D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
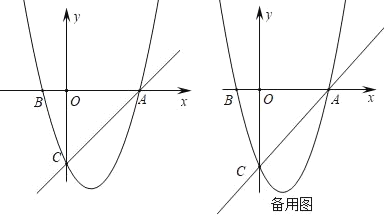
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.
(1)求抛物线的解析式;
(2)若动点P在第四象限内的抛物线上,过动点P作x轴的垂线交直线AC于点D,交x轴于点E,垂足为E,求线段PD的长,当线段PD最长时,求出点P的坐标;
(3)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com