【题目】
中，
，
边的垂直平分线交直线BC于点E，若
，
．则
的值为__________．
【答案】3或
【解析】
通过题干信息点E在直线BC上可知，需分情况讨论，再画出几何图形，利用线段垂直平分线定理，构造全等三角形进行线段转化，进而求得目标角的正切值．
解：当
的垂直平分线交线段BC于点E时，如图交AC于点D，连AE，
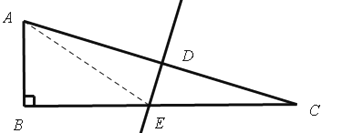
∴AD=DC，且
，
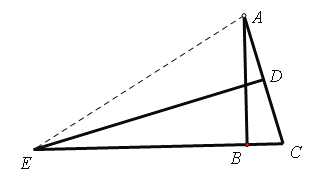
∴在△ADE和△CDE中，
，
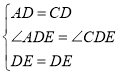∴△ADE≌△CDE，
∴AE=EC，
又∵
，
，
，
∴
，
∴EC=5，
∴BC=BE+EC=4+5=9，
∴
；
当
的垂直平分线交CB的延长线于点E时，如图交AC于点D，连AE，
∴AD=DC，且，DE=DE，
∴△ADE≌△CDE，
∴AE=EC，
∵，，，
∴，
∴EC=5，
∴BC=EC-EB=5-4=1，
∴
，
综上：
的值为或3，
故答案为：或3．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图1，在Rt△ABC中，∠ACB=90°，点P以每秒1cm的速度从点A出发，沿折线AC－CB运动，到点B停止．过点P作PD⊥AB，垂足为D，PD的长y（cm）与点P的运动时间x（秒）的函数图象如图2所示．当点P运动5秒时，PD的长是（ ）
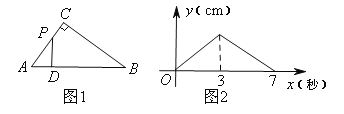
A.1.5cmB.1.2cmC.1.8cmD.2cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如图（1），
，
，
，
四点分别在四边形
的四条边上，若四边形
为菱形，我们称菱形为四边形的内接菱形.
动手操作：
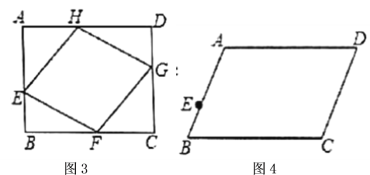
（1）如图2，网格中的每个小四边形都为正方形，每个小四边形的顶点叫做格点，由
个小正方形组成一个大正方形，点、在格点上，请在图（2）中画出四边形的内接菱形；
特例探索：
（2）如图3，矩形，
，点在线段
上且
，四边形是矩形的内接菱形，求
的长度；
拓展应用：
（3）如图4，平行四边形，，
，点在线段上且，
①请你在图4中画出平行四边形的内接菱形，点在边
上；
②在①的条件下，当
的长最短时，的长为__________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点C是⊙O上一点，AC平分∠DAB，直线DC与AB的延长线相交于点P，AD与PC延长线垂直，垂足为D，CE平分∠ACB，交⊙O于E．
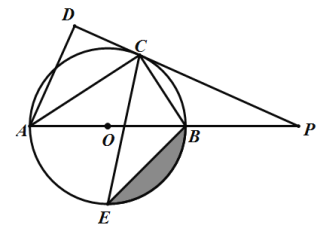
（1）求证：PC与⊙O相切；
（2）若AC=6，tan∠BEC=
，求BE的长度以及图中阴影部分面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
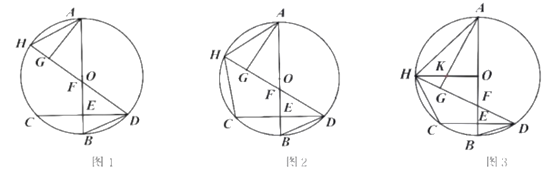
【题目】已知：如图，AB为
的直径，弦
垂足为E，点H为弧AC上一点．连接DH交AB于点F，连接HA、BD，点G为DH上一点，连接AG，
．
（1）如图1，求证：
；
（2）如图2，连接HC，若
，求证：
；
（3）如图3，连接
交
于点K，若点F为DG的中点，
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
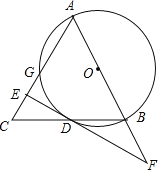
【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，交AC于点G，过D作EF⊥AC于点E，交AB的延长线于点F．
（1）求证：EF是⊙O的切线；
（2）当∠BAC＝60°，AB＝8时，求EG的长；
（3）当AB＝5，BC＝6时，求tanF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，AB是半圆O的直径，AC是弦，点P沿BA方向，从点B运动到点A，速度为1cm/s，若AB=10cm，点O到AC的距离为4cm．
（1）求弦AC的长；
（2）问经过多长时间后，△APC是等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解初一年级学生每学期参加综合实践活动的情况，某区教育行政部门随机抽样调查了部分初一学生一个学期参加综合实践活动的天数，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：
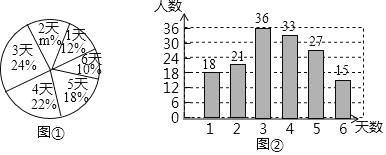
（I）本次随机抽样调查的学生人数为 ，图①中的m的值为 ；
（II）求本次抽样调查获取的样本数据的众数、中位数和平均数；
（III）若该区初一年级共有学生2500人，请估计该区初一年级这个学期参加综合实践活动的天数大于4天的学生人数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
