
 海轮以每小时30nmile的速度航行,在点A处测得海上油井P在它的南偏东60°方向,向北航行40min后到达B处,测得油井P在南偏东30°方向,海轮改北偏东60在再航行120min到达C处,求P,C间的距离及此时点C在油井P的什么方向.
海轮以每小时30nmile的速度航行,在点A处测得海上油井P在它的南偏东60°方向,向北航行40min后到达B处,测得油井P在南偏东30°方向,海轮改北偏东60在再航行120min到达C处,求P,C间的距离及此时点C在油井P的什么方向. 分析 根据题意和锐角三角函数可以求得PD和BD的长,从而可以求得BP的长,然后根据勾股定理即可求得PC的长,再根据锐角三角函数可以求得∠BPC的度数,从而可以解答本题.
解答 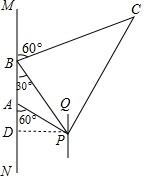 解:作PD⊥BA交BA的延长线于点D,
解:作PD⊥BA交BA的延长线于点D,
由题意可得,
tan30°=$\frac{DP}{BD}$,tan60°=$\frac{DP}{AD}$,AB=40,BC=30×(120÷60)=60,
解得,AD=20,DP=20$\sqrt{3}$,
∴BP=$\frac{DP}{sin30°}$=40$\sqrt{3}$,
∵∠CBP=90°,BC=60,BP=40$\sqrt{3}$,
∴PC=$\sqrt{B{C}^{2}+B{P}^{2}}$=20$\sqrt{21}$
tan∠BPC=$\frac{BC}{BP}$=$\frac{60}{40\sqrt{3}}=\frac{\sqrt{3}}{2}$,
∴∠BPC≈41°,
∴此时点C在油井P的北偏东41°-30°=11°方向,
即P,C间的距离是20$\sqrt{21}$nmile,此时点C在油井P的北偏东11°方向.
点评 本题考查解直角三角形的应用-方向角问题、勾股定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用解直角三角形的相关知识解答.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )| A. | 2$\sqrt{2}$<r<$\sqrt{17}$ | B. | $\sqrt{17}$<r≤3$\sqrt{2}$ | C. | $\sqrt{17}$<r<5 | D. | 5<r<$\sqrt{29}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,则这个陀螺的表面积是( )
“赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm,圆柱体部分的高BC=6cm,圆锥体部分的高CD=3cm,则这个陀螺的表面积是( )| A. | 68πcm2 | B. | 74πcm2 | C. | 84πcm2 | D. | 100πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
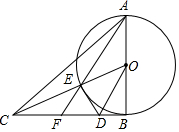 如图,等腰直角△ABC中,∠ABC=90°,以AB为直径作⊙O,连接OC交⊙O于E,AE交BC于点F,过O作OD∥AF交BC于D,连接DE.
如图,等腰直角△ABC中,∠ABC=90°,以AB为直径作⊙O,连接OC交⊙O于E,AE交BC于点F,过O作OD∥AF交BC于D,连接DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com