
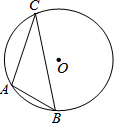
 如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB长4cm.
如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB长4cm. 科目:初中数学 来源: 题型:选择题
 如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )
如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是( )| A. | $\frac{4π}{3}$$-\sqrt{3}$ | B. | $\frac{4π}{3}$-2$\sqrt{3}$ | C. | $\frac{2π}{3}$$-\sqrt{3}$ | D. | $\frac{2π}{3}$-$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 海轮以每小时30nmile的速度航行,在点A处测得海上油井P在它的南偏东60°方向,向北航行40min后到达B处,测得油井P在南偏东30°方向,海轮改北偏东60在再航行120min到达C处,求P,C间的距离及此时点C在油井P的什么方向.
海轮以每小时30nmile的速度航行,在点A处测得海上油井P在它的南偏东60°方向,向北航行40min后到达B处,测得油井P在南偏东30°方向,海轮改北偏东60在再航行120min到达C处,求P,C间的距离及此时点C在油井P的什么方向.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,2) | B. | (-4,2) | C. | (-1,5) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
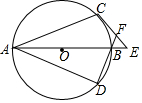 如图,AB为⊙O的直径,AC,AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为3,∠E=45°,则CF的长为6-3$\sqrt{2}$.
如图,AB为⊙O的直径,AC,AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为3,∠E=45°,则CF的长为6-3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
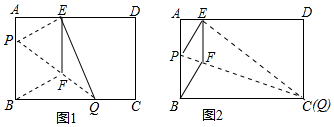
 已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.
已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com