
【题目】如图,在⊙O中,点C为![]() 的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.
的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.
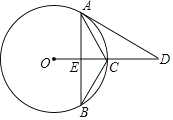
(1)求证:AD与⊙O相切;
(2)若CE=4,求弦AB的长.
【答案】(1)见解析;(2)8![]()
【解析】
(1)连接OA,由![]() ,得CA=CB,根据题意可得出∠O=60°,从而得出∠OAD=90°,则AD与⊙O相切;
,得CA=CB,根据题意可得出∠O=60°,从而得出∠OAD=90°,则AD与⊙O相切;
(2)由题意得OC⊥AB,Rt△BCE中,由三角函数得BE=4![]() ,即可得出AB的长.
,即可得出AB的长.
(1)证明:如图,连接OA,
∵![]() ,
,
∴CA=CB,
又∵∠ACB=120°,
∴∠B=30°,
∴∠O=2∠B=60°,
∵∠D=∠B=30°,
∴∠OAD=180°﹣(∠O+∠D)=90°,
∴AD与⊙O相切;
(2)∵∠O=60°,OA=OC,
∴△OAC是等边三角形,
∴∠ACO=60°,
∵∠ACB=120°,
∴∠ACB=2∠ACO,AC=BC,
∴OC⊥AB,AB=2BE,
∵CE=4,∠B=30°,
∴BC=2CE=8,
∴BE=![]() =
=![]() =4
=4![]() ,
,
∴AB=2BE=8![]() ,
,
∴弦AB的长为8![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
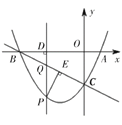
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上的一个动点,过
是抛物线上的一个动点,过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)直接写出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(2)若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求此时点
为顶点的四边形是平行四边形,求此时点![]() 的坐标;
的坐标;
(3)当点![]() 位于直线
位于直线![]() 下方的抛物线上时,过点
下方的抛物线上时,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
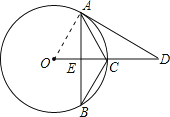
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
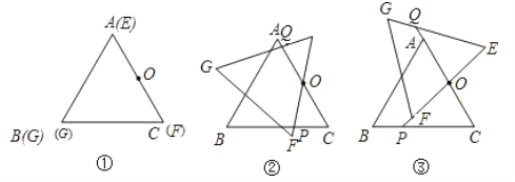
【题目】△ABC和△EFG是两块完全重合的等边三角形纸片,(如图①所示)O是AB(或EF)的中点,△ABC不动,将△EFG绕O点顺时针转α﹝0°<α<120°﹞角.
(1)试分别说明α为多少度时,点F在△ABC外部、BC上、内部(不证明)?
(2)当点F不在BC上时,在图②、图③两种情况下(设EF或延长线与BC交于P,EG与CA或延长线交于Q),分别写出OP与OQ的数量关系,并将图③情况给予说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有![]() 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
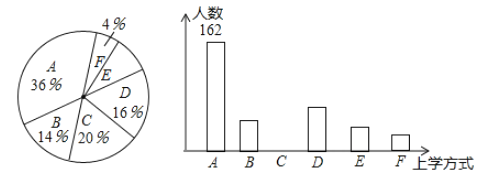
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择![]() 类的人数有_____人;
类的人数有_____人;
(2)在扇形统计图中,求![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)若将![]() 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某县政府部门决定,招标一工程队负责完成一座水库的土方施工任务.该工程队有A,B两种型号的挖掘机,已知1台A型和2台B型挖掘机同时施工1小时共挖土80立方米,2台A型和3台B型挖掘机同时施工1小时共挖土140立方米.每台A型挖掘机一个小时的施工费用是350元,每台B型挖掘机一个小时的施工费用是200元.
(1)分别求每台A型,B型挖掘机一小时各挖土多少立方米?
(2)若A型和B型挖掘机共10台同时施工4小时,至少完成1360立方米的挖土量,且总费用不超过14000元.问施工时有哪几种调配方案?且指出哪种调配方案的施工费用最低,最低费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠ABC=90°,AB=9,BC=12.点Q是线段AC上的一个动点,过点Q作AC的垂线交射线AB于点P.当△PQB为等腰三角形时,则AP的长为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com