
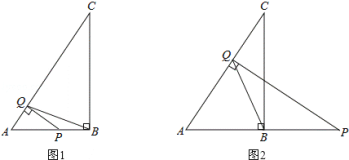
【题目】已知在△ABC中,∠ABC=90°,AB=9,BC=12.点Q是线段AC上的一个动点,过点Q作AC的垂线交射线AB于点P.当△PQB为等腰三角形时,则AP的长为_______.
【答案】5或18
【解析】
当△PQB为等腰三角形时,有两种情况: ①当点P在线段AB上时,如题图1所示.由△AQP∽△ABC即可计算AP的长;②当点P在线段AB的延长线上时,如题图2所示,利用角之间的关系,证明点B为线段AP的中点,从而可以求出AP.
∵∠A+∠APQ=90°,∠A+∠C=90°,
∴∠APQ=∠C.
∵∠A=∠A,
∴△APQ∽△ACB.
在Rt△ABC中,AB=9,BC=12,由勾股定理得:AC=15,
①当点P在线段AB上时,如题图1所示,
∵∠BPQ为钝角,
∴当△PQB为等腰三角形时,只可能是PB=PQ.
∵△APQ∽△ACB,
∴![]() ,即
,即![]() ,解得:PB=4,
,解得:PB=4,
∴AP=AB﹣PB=9-4=5;
②当点P在线段AB的延长线上时,如题图2所示,
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,只可能是BP=BQ,
∴∠BQP=∠P,
∵∠BQP+∠AQB=90°,∠A+∠P=90°,
∴∠AQB=∠A,
∴BQ=AB,
∴AB=BP,点B为线段AB中点,
∴AP=2AB=2×9=18.
综上所述,当△PQB为等腰三角形时,AP的长为5或18.
故答案是:5或18.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点C为![]() 的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.
的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.
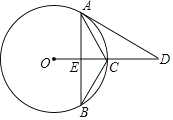
(1)求证:AD与⊙O相切;
(2)若CE=4,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
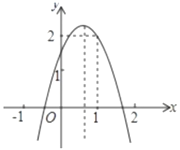
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() 且与
且与![]() 轴交点的横坐标分别为
轴交点的横坐标分别为![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中结论正确的有( ).
,其中结论正确的有( ).
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
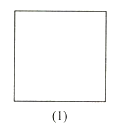
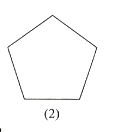
【题目】试比较图中两个几何图形的异同,请分别写出它们的两个相同点和两个不同点。例如,相同点:正方形的对角线相等,正五边形的。对角线也相等;不同点:正方形是中心对称图形,正五边形不是中心对称图形。
相同点:①_________________;②___________________
不同点:①______________________;②____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 为常数).
为常数).
(1)当![]() ,
,![]() 时,求二次函数的最小值;
时,求二次函数的最小值;
(2)当![]() 时,若在函数值
时,若在函数值![]() 的情况下,只有一个自变量
的情况下,只有一个自变量![]() 的值与其对应,求此时二次函数的解析式;
的值与其对应,求此时二次函数的解析式;
(3)当![]() 时,若在自变量
时,若在自变量![]() 的值满足
的值满足![]() ≤
≤![]() ≤
≤![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最小值为21,求此时二次函数的解析式.
的最小值为21,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中
中![]() ,
,![]() ,
,![]() 点P从点B出发,沿折线
点P从点B出发,沿折线![]() 运动,当它到达点A时停止,设点P运动的路程为
运动,当它到达点A时停止,设点P运动的路程为![]() 点Q是射线CA上一点,
点Q是射线CA上一点,![]() ,连接
,连接![]() 设
设![]() ,
,![]() .
.
![]() 求出
求出![]() ,
,![]() 与x的函数关系式,并注明x的取值范围;
与x的函数关系式,并注明x的取值范围;
![]() 补全表格中
补全表格中![]() 的值;
的值;
x | 1 | 2 | 3 | 4 | 6 |
| ______ | ______ | ______ | ______ | ______ |
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,并在x的取值范围内画出![]() 的函数图象:
的函数图象:
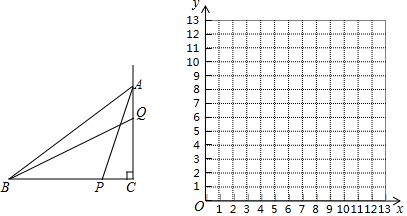
![]() 在直角坐标系内直接画出
在直角坐标系内直接画出![]() 函数图象,结合
函数图象,结合![]() 和
和![]() 的函数图象,求出当
的函数图象,求出当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
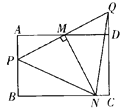
【题目】在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;
②请问![]() 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
是否为定值?若是定值,求出该定值;若不是,请举反例说明;
(2)当△PBN与△NCQ的面积相等时,求AP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月12日是“母亲节”,某校开展“感恩母亲,做点家务”活动为了了解同学们在母亲节这一天做家务情况,学校随机抽查了部分同学,并用得到的数据制成如下不完整的统计表:
做家务时间(小时) | 人数 | 所占百分比 |
| 15 | 30% |
| 31 | 62% |
|
| 4% |
| 2 |
|
合计 |
| 100% |
(1)统计表中的![]() __________,
__________,![]() __________;
__________;
(2)小君计算被抽查同学做家务时间的平均数是这样的:
第一步:计算平均数的公式是![]() ,
,
第二步:该问题中![]() ,
,![]()
![]() ,
,![]() ,
,![]() ;
;
第三步:![]() (小时)
(小时)
小君计算的过程正确吗?如果不正确,请你计算出正确的做家务时间的平均数;
(3)现从![]() ,
,![]() 两组中任选2人,求这2人都在
两组中任选2人,求这2人都在![]() 组中的概率(用树形图法或列表法).
组中的概率(用树形图法或列表法).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com