
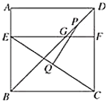
【题目】如图,正方形![]() 的边长为12,点
的边长为12,点![]() 在边
在边![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点.若点
两点.若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,则
的中点,则![]() 的长为________.
的长为________.
科目:初中数学 来源: 题型:
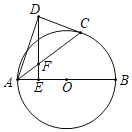
【题目】如图,AB是⊙O的直径,点C在半圆上,点D在圆外,DE⊥AB于点E交AC于点F,且DF=CD
(1)求证:CD是⊙O的切线;
(2)若点F是AC的中点,DF=2EF=2![]() ,求⊙O半径.
,求⊙O半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
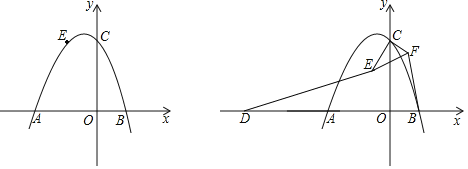
【题目】如图抛物线y=ax2+ax+c(a≠0)与x轴的交点为A、B(A在B的左边)且AB=3,与y轴交于C,若抛物线过点E(﹣1,2).
(1)求抛物线的解析式;
(2)在x轴的下方是否存在一点P使得△PBC的面积为3?若存在求出P点的坐标,不存在说明理由;
(3)若D为原点关于A点的对称点,F点坐标为(0,1.5),将△CEF绕点C旋转,在旋转过程中,线段DE与BF是否存在某种关系(数量、位置)?请指出并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
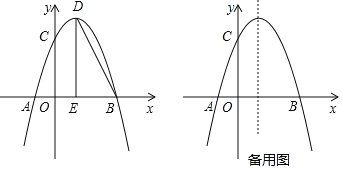
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B,与y轴交于点C,且OA=2,OB=OC=6,点D是抛物线的顶点,过点D作x轴的垂线,垂足为E.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,若点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标:
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
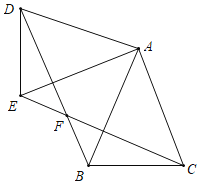
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()
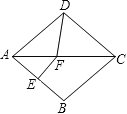
A.50°B.60°C.70°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
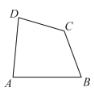
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”,例如:如图,四边形![]() 是“等对角四边形”,
是“等对角四边形”,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
(1)已知:在“等对角四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,求对角线
,求对角线![]() 的长;
的长;
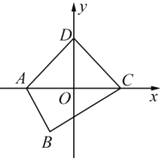
(2)已知:如图,在平面直角坐标系![]() 中,四边形
中,四边形![]() 是“等对角四边形”,其中
是“等对角四边形”,其中![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,抛物线
轴上,抛物线![]() 过点
过点![]() 、
、![]() ,点
,点![]() 在抛物线上,满足
在抛物线上,满足![]() 的
的![]() 点至少有3个时,总有不等式
点至少有3个时,总有不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com