练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．修筑一条公路，需要运输大量沙石，某运输队有载重量为8吨的卡车5辆，载重量为10吨的卡车有7辆，为了工程尽早完工，需要一次运输的沙石达到165吨以上，为了完成任务，该运输队准备新增购这两种卡车共6辆，车队有多少种购买方案，请你一一列举．

    分析 利用“需要一次运输沙石165吨以上”得出不等式求出购买方案即可．

    解答 解：设载重量为8吨的卡车增加了x辆，
    依题意得：8（5+x）+10（7+6-x）＞165，
    解得：x＜2.5，
    ∵x≥0且为整数，
    ∴x=0，1，2；
    ∴6-x=6，5，4．
    ∴车队共有3种购车方案：
    ①载重量为8吨的卡车购买1辆，10吨的卡车购买5辆；
    ②载重量为8吨的卡车购买2辆，10吨的卡车购买4辆；
    ③载重量为8吨的卡车不购买，10吨的卡车购买6辆．

    点评 此题主要考查了不等式的应用，根据已知得出正确的不等式关系是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

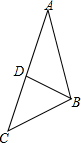    2．如图，在△ABC中，D是边AC上一点，连BD，给出下列条件：①∠ABD=∠ACB；②AB2=AD•AC；③AD•BC=AB•BD；④AB•BC=AC•BD．其中单独能够判定△ABC∽△ADB的个数是（　　）
    A．①②B．①②③C．①②④D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．读故事学数学，从前，有一位老人在临终前立下遗嘱，遗嘱上写着：“我把十七匹马全都留给我的三个儿子，长子得一半，次子得$\frac{1}{3}$，给幼子$\frac{1}{9}$．不许流血，不许杀马．你们必须遵从父亲的意愿！”老人去世后，三个兄弟对分马一事迷惑不解，他们九区请教当地一位公认的智者，这位智者看了遗嘱以后说：“我借给你们一匹马，去按你们父亲的遗嘱分吧！”于是三兄弟按照老人的遗嘱，分别得到了九匹、六匹和两匹，最后还剩下一匹，是智者借给他们的那匹，还给智者，这种分马的方法我们把它称为“借一还一法”，“借一还一法”在数学上有着很重的应用，如在计算（2+1）（22+1）（24+1）（28+1）时，因没有两数之差，因此可借（2-1），然后连续利用平方差公式来计算．请你仿照这种方法计算：（1+$\frac{1}{2}$）×（1+$\frac{1}{{2}^{2}}$）×（1+$\frac{1}{{4}^{2}}$）×（1+$\frac{1}{{2}^{8}}$）+$\frac{1}{{2}^{15}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．关于x的方程$\frac{1}{a}+\frac{1}{b}=\frac{1}{x}$（a+b≠0）的解为x=$\frac{ab}{a+b}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

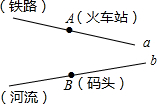    7．火车站，码头分别位于A，B两点，直线a，b分别表示铁路与河流
    （1）从火车站到码头怎样走最近？
    （2）从码头到铁路怎样走最近？请画图并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解方程组：$\left\{\begin{array}{l}{3x+6y=13}\\{-5x-13y=24}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．因式分解：x2-ax-bx+ab．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．对于某些三角形或是四边形，我们可以直接用面积公式或是用割补法等来求它们的面积，下面我们研究一种求面积的新方法：
    如图1、2所示，分别过三角形或是四边形的顶点A、C作水平线的铅垂线l1、l2，l1、l2之间的距离d叫做水平宽；如图1所示，过点B作水平线的铅垂线交AC于点D，称线段BD的长叫做这个三角形的铅垂高；如图2所示，分别过四边形的顶点B、D作水平线l3、l4，l3、l4之间的距离h叫做四边形的铅垂高．

    【结论提炼】：容易证明：“三角形的面积等于水平宽与铅垂高乘积的一半”，即“S=$\frac{1}{2}$dh”．
    【尝试应用】：
    已知：如图3，点A（-5，2）、B（5，0）、C（0，5），则△ABC的水平宽为10，铅垂高为5，所以△ABC的面积为25．
    【再探新知】：

    三角形的面积可以用“水平宽与铅垂高乘积的一半”来求，那四边形的面积是不是也可以这样求呢？带着这个问题，小明进行了如下探索尝试：
    （1）他首先在图4所示的平面直角坐标系中，取了A（-4，2）、B（1，5）、C（4，1）、D（-1，-4）四个点，得到了四边形ABCD．
    小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是36；他又用其它的方法进行了计算，结果是37，由此他发现：用“S=$\frac{1}{2}$dh”这一方法对图4中的四边形求面积不适合（填“适合”或“不适合”）．

    （2）小明并没有放弃尝试，他又在图5所示的平面直角坐标系中，取了A（-5，2）、B（1，5）、C（4，2）、D（-1，-3）四个点，得到了四边形ABCD．小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是36，由此他发现：用“S=$\frac{1}{2}$dh”这一方法对图5中的四边形求面积适合（填“适合”或“不适合”）．
    （3）小明很奇怪，就继续进行了进一步尝试，他在图6所示的平面直角坐标系中，取了A（-4，2）、B（1，5）、C（5，1）、D（1，-5）四个点，得到了四边形ABCD．通过计算他发现：用“S=$\frac{1}{2}$dh”这一方法对图6中的四边形求面积适合（填“适合”或“不适合”）．
    通过以上尝试，小明恍然大悟得出结论：当四边形满足一条对角线等于水平宽或铅垂高条件时，四边形可以用“S=$\frac{1}{2}$dh”来求面积．
    【学以致用】：
    如图7，在平面直角坐标系中，点M坐标为（-2，0），抛物线的解析式为：y=$\frac{1}{4}$x2-2x+3，抛物线图象与y轴交于点A，与x轴交于B、C两点，点P为抛物线上一点，且位于B、C之间，请直接运用以上结论，写出当点P坐标为多少时，四边形AMPC面积最大．（直接写出P点坐标即可）

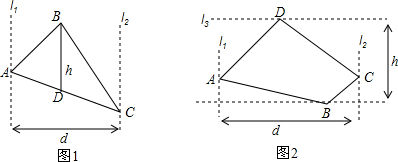
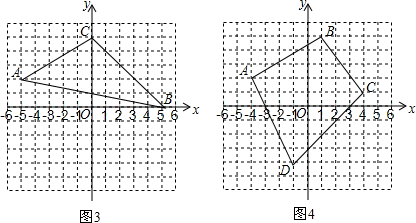
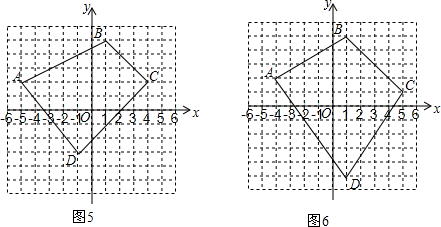
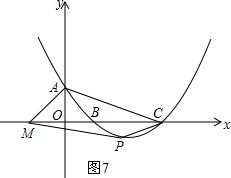
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列说法正确的是（　　）
    A．一组数据8，8，7，10，6，8，9的众数和中位数都是8
    B．为了解全国中学生的心理健康情况，应该采用普查的方式
    C．一个游戏的中奖概率是0.1，则做10次这样的游戏一定会中奖
    D．若甲组数据的方差s2=0.01，乙组数据的方差s2=0.1，则乙组数据比甲组数据稳定

    查看答案和解析>>

    同步练习册答案