
【题目】阅读下面内容,并按要求解决问题:
问题:“在平面内,已知分别有2个点,3个点,4个点,5个点,…,![]() 个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
探究:为了解决这个问题,希望小组的同学们,设计了如下表格进行探究:(为了方便研究问题,图中每条线段表示过线段两端点的一条直线)
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为______;
个点时,直线条数为______;
(2)若某同学按照本题中的方法,共画了28条直线,求该平面内有多少个已知点?
科目:初中数学 来源: 题型:
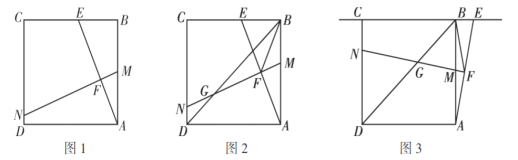
【题目】综合与探究如图,在正方形![]() 中,点
中,点![]() 在
在![]() 边所在的直线上运动但不与点
边所在的直线上运动但不与点![]() 重合,点
重合,点![]() 在线段
在线段![]() .上运动,过点
.上运动,过点![]() 的直线
的直线![]() ,分别交
,分别交![]() 于点
于点![]() .
.
观察探究:(1)如图1,当点![]() 在边
在边![]() 上时,判断并说明
上时,判断并说明![]() 与
与![]() 的数量关系;
的数量关系;
探究发现:(2)勤奋小组在图1的基础上得到图2,点![]() 为
为![]() 中点时,其他条件不变,连接正方形的对角线
中点时,其他条件不变,连接正方形的对角线![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,此时,
,此时,![]() ,请利用图2证明;
,请利用图2证明;
探究拓展:(3)如图3,缜密小组在勤奋小组的启发下,当点![]() 在点
在点![]() 右侧时,如果(2)中的其他条件不变,直线
右侧时,如果(2)中的其他条件不变,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,他们发现线段
,他们发现线段![]() 与
与![]() 之间存在数量关系,线段
之间存在数量关系,线段![]() 与
与![]() 之间也存在数量关系,请你直接写出.
之间也存在数量关系,请你直接写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣![]() x+c与直线y=
x+c与直线y=![]() x+
x+![]() 交于A、B两点,已知点B的横坐标是4,直线y=
交于A、B两点,已知点B的横坐标是4,直线y=![]() x+
x+![]() 与x、y轴的交点分别为A、C,点P是抛物线上一动点.
与x、y轴的交点分别为A、C,点P是抛物线上一动点.
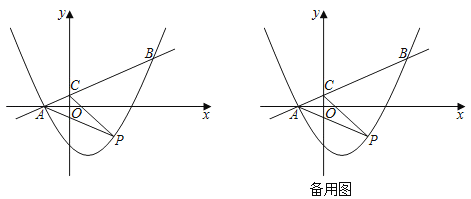
(1)求抛物线的解析式;
(2)若点P在直线y=![]() x+
x+![]() 下方,求△PAC的最大面积;
下方,求△PAC的最大面积;
(3)设M是抛物线对称轴上的一点,以点A、B、P、M为顶点的四边形能否成为平行四边形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
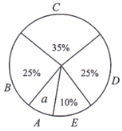
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆轿车从甲地驶往乙地,到达乙地后返回甲地,速度是原来的1.5倍,共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶.设轿车行驶的时间为x(h),两车到甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图.
(1)求轿车从乙地返回甲地时的速度和t的值;
(2)求轿车从乙地返回甲地时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)直接写出轿车从乙地返回甲地时与货车相遇的时间.
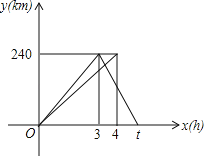
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西汾酒,又称“杏花村酒”.酿造汾酒是选用晋中平原的“一把抓高粱”为原料.汾阳县某村民合作社2016年种植“一把抓高粱”100亩,2018年该合作社扩大了“一把抓高梁”的种植面积,共种植144亩.
(1)求该合作社这两年种植“一把抓高梁”亩数的平均增长率;
(2)某粮店销售“一把抓高粱”售价为13元/斤,每天可售出30斤,每斤的盈利是1.5元.为了减少库存,粮店决定搞促销活动.在销售中发现:售价每降价0.1元,则可多售出2斤.若该粮店某天销售“一把抓高梁”的盈利为40元,则该店当天销售单价降低了多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量小岛A到公路BD的距离,先在点B处测得∠ABD=37°,再沿BD方向前进150m到达点C,测得∠ACD=45°,求小岛A到公路BD的距离.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
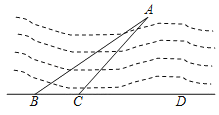
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意一个四位数![]() .如果把它的前两位数字和后两位数字调换,则称得到的数为
.如果把它的前两位数字和后两位数字调换,则称得到的数为![]() 的调换数,把
的调换数,把![]() 与其调换数之差记为
与其调换数之差记为![]() ,例如
,例如![]() 的调换数为
的调换数为![]() ,
,![]() .
.
(1)求证:对于任意![]() 一个四位数
一个四位数![]() ,
,![]() 都能被
都能被![]() 整除.
整除.
(2)我们把![]() 与
与![]() 的商记为
的商记为![]() ,例如
,例如![]() ,若有两数
,若有两数![]() 、
、![]() ,其中
,其中![]() ,
, ![]() ,
,![]() ,
,![]() 、
、![]() 都是正整数),那么当
都是正整数),那么当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小风筝与一个大风等形状完全相同,它们的形状如图所示,其中对角线AC⊥BD.已知它们的对应边之比为1:3,小风筝两条对角线的长分別为12cm和14cm.

(1)小风筝的面积是多少?
(2)如果在大风筝内装设一个连接对角顶点的十字交叉形的支撑架,那么至少需用多长的材料?(不记损耗)
(3)大风筝要用彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com