
【题目】对任意一个两位数m,如果m等于两个正整数的平方和,那么称这个两位数m为“平方和数”,若m=a2+b2(a、b为正整数),记A(m)=ab.例如:29=22+52,29就是一个“平方和数”,则A(29)=2×5=10.
(1)判断25是否是“平方和数”,若是,请计算A(25)的值;若不是,请说明理由;
(2)若k是一个“平方和数”,且A(k)=![]() ,求k的值.
,求k的值.
【答案】(1)25是“平方和数”,A(25)=12;(2)k的值为10或20或34或52或74
【解析】
(1)把25写成两个正整数的平方和,再根据A(m)=ab求出A(25)便可;
(2)设k=a2+b2,则A(k)=ab,根据(k)=![]() ,得a、b的方程,求得a与b的关系式,进而由a、b、k满足的条件求得k的值便可.
,得a、b的方程,求得a与b的关系式,进而由a、b、k满足的条件求得k的值便可.
(1)25是“平方和数”
∵25=32+42
∴A(25)=3×4=12
故答案为:25是“平方和数”,A(25)=12
(2)设k=a2+b2,则A(k)=ab
∵A(k)=![]()
∴ab=![]()
∴2ab=a2+b2﹣4
∴a2﹣2ab+b2=4
∴(a﹣b)2=4
∴a﹣b=±2,即a=b+2或b=a+2,
∵a、b为正整数,k为两位数,
∴当a=1,b=3或a=3,b=1时,k=10;
当a=2,b=4或a=4,b=2时,k=20;
当a=3,b=5或a=5,b=3时,k=34;
当a=4,b=6或a=6,b=4时,k=52;
当a=5,b=7或a=7,b=5时,k=74;
综上,k的值为:10或20或34或52或74.
故答案为:k的值为10或20或34或52或74


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm,点P为边AC上一点,且AP=5cm.点Q为边AB上的任意一点(不与点A,B重合),若点A关于直线PQ的对称点A'恰好落在△ABC的边上,则AQ的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
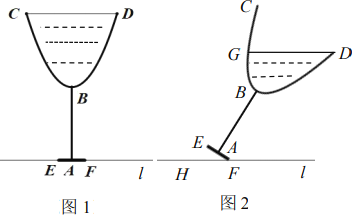
【题目】图1是一个高脚杯截面图,杯体![]() 呈抛物线状(杯体厚度不计),点
呈抛物线状(杯体厚度不计),点![]() 是抛物线的顶点,
是抛物线的顶点,![]() ,点
,点![]() 是
是![]() 的中点,当高脚杯中装满液体时,液面
的中点,当高脚杯中装满液体时,液面![]() ,此时最大深度(液面到最低点的距离)为
,此时最大深度(液面到最低点的距离)为![]() ,将高脚杯绕点
,将高脚杯绕点![]() 缓缓倾斜倒出部分液体,当
缓缓倾斜倒出部分液体,当![]() 时停止,此时液面为
时停止,此时液面为![]() ,则液面
,则液面![]() 到平面
到平面![]() 的距离是________________;此时杯体内液体的最大深度为_____________________.
的距离是________________;此时杯体内液体的最大深度为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
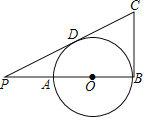
A.1.5B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
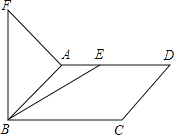
【题目】如图,在平行四边形ABCD中,AB=2,∠ABC=45°,点E为射线AD上一动点,连接BE,将BE绕点B逆时针旋转60°得到BF,连接AF,则AF的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸板和圆形纸板按如图方式分别剪得同样大定理特例图(AC=3,BC=4,AB=5,分别以三边长向外剪正方形) ,图1中边HI、LM和点K、J都恰好在矩形纸板的边上,图2中的圆心O在AB中点处,点H、I都在圆上,则矩形和圆形纸板的面积比是( )
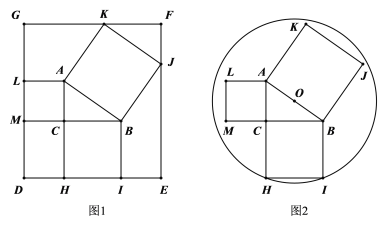
A.400:127πB.484:145πC.440:137πD.88:25π
查看答案和解析>>
科目:初中数学 来源: 题型:
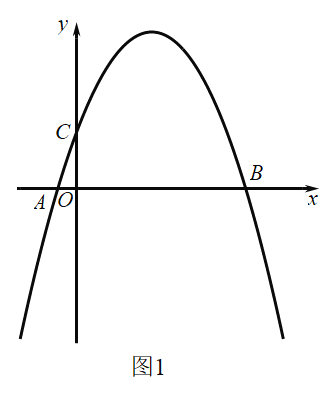
【题目】已知:在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右边)交
的右边)交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)如图1,求抛物线的解析式;
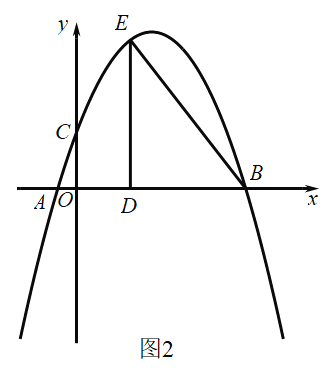
(2)如图2,点![]() 是第一象限抛物线上的点,连接
是第一象限抛物线上的点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
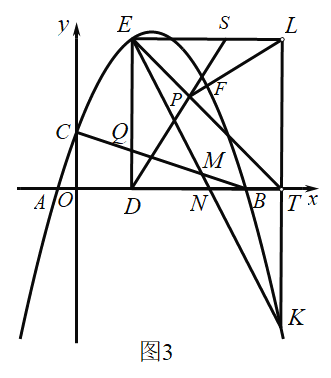
(3)如图3,在(2)的条件下,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是第四象限抛物线上的点,连接
是第四象限抛物线上的点,连接![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,点
,点![]() 是抛物线对称轴右侧第一象限抛物线上的点,连接
是抛物线对称轴右侧第一象限抛物线上的点,连接![]() 、
、![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() .求点
.求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
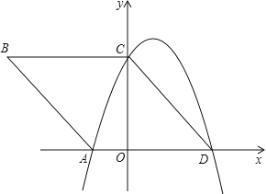
【题目】如图,在平面直角坐标系xOy中,四边形ABCD是边长为5的菱形,顶点A.C.D均在坐标轴上,sinB=![]() .
.
(1)求过A,C,D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1>y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A,E两点之间的一个动点,且直线PE交x轴于点F,问:当P点在何处时,△PAE的面积最大?并求出面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com