
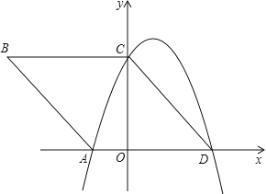
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У��ı���ABCD�DZ߳�Ϊ5�����Σ�����A��C��D�����������ϣ�sinB=![]() ��
��
��1�����A��C��D����������ߵĽ���ʽ��
��2����ֱ��AB�Ľ���ʽΪy1=mx+n����1���������ߵĽ���ʽΪy2=ax2+bx+c����y1>y2ʱ���Ա���x��ȡֵ��Χ��
��3����ֱ��AB�루1���������ߵ���һ������ΪE��P��Ϊ��������A��E����֮���һ�����㣬��ֱ��PE��x���ڵ�F���ʣ���P���ںδ�ʱ����PAE�������������������ֵ��
���𰸡���1��y=��![]() x2+
x2+![]() x+4����2��x��-2��x��5����3����P(
x+4����2��x��-2��x��5����3����P(![]() ��
��![]() )ʱ����PAE��������������Ϊ
)ʱ����PAE��������������Ϊ![]()
��������
��1��������ABCD�ı߳���һ�ǵ�����ֵ�������OC��OD��OA�ij�������ȷ��A��C��D�������꣬ͨ������ϵ��������������ߵĽ���ʽ��
��2��������A��B������ȷ��ֱ��AB�Ľ���ʽ��Ȼ�����ֱ��AB�������߽���ʽ���������㣬Ȼ��ͨ���۲�ͼ���ҳ�ֱ��y1��������y2ͼ���·��IJ��֣�
��3������Ĺؼ�����ȷ����P��λ�ã���APE����������ôS��APE=![]() AE��h��h��ֵ�����P��ֱ��AE�ľ�����Զ����ô��PΪ��ֱ��ABƽ���������������ҽ��е�Ψһ���㣮
AE��h��h��ֵ�����P��ֱ��AE�ľ�����Զ����ô��PΪ��ֱ��ABƽ���������������ҽ��е�Ψһ���㣮
�⣺��1�����ı���ABCD�DZ߳�Ϊ5�����Σ���AB=AD=CD=BC=5��sinB=sinD=![]() ��
��
Rt��OCD��OC=CDsinD=4��OD=3��OA=AD��OD=2������
A����2��0����B����5��4����C��0��4����D��3��0����
�������ߵĽ���ʽΪ��y=a��x+2����x��3�����ã�2������3��a=4��a=![]() ��
��
�������ߣ�y=��![]() x2+
x2+![]() x+4��
x+4��
��2����A����2��0����B����5��4����ֱ��AB��y1=��![]() x��
x��![]() ��
��
�ɣ�1���ã�y2=��![]() x2+
x2+![]() x+4����
x+4����
 ����ã�
����ã� ��
�� ��
��
��ͼ��֪����y1>y2ʱ��x&l;-2��x>5��
��3����S��APE=![]() AEh������P��ֱ��AB�ľ�����Զʱ��S��ABE���
AEh������P��ֱ��AB�ľ�����Զʱ��S��ABE���
����ֱ��L��AB����ֱ��L������������ֻ��һ������ʱ���ý��㼴Ϊ��P��
��ֱ��L��y=��![]() x+b����ֱ��L������������ֻ��һ������ʱ��
x+b����ֱ��L������������ֻ��һ������ʱ��
��![]() x+b=��
x+b=��![]() x2+
x2+![]() x+4������=0����ã�b=
x+4������=0����ã�b=![]() ����ֱ��L��y=��
����ֱ��L��y=��![]() x+
x+![]() ��
��
�ɵõ�P��![]() ��
��![]() �����ɣ�2���ã�E��5����
�����ɣ�2���ã�E��5����![]() ������ֱ��PE��y=��
������ֱ��PE��y=��![]() x+9��
x+9��
PE��x��Ľ���F������Ϊ��![]() ��0����AF=OA+OF=
��0����AF=OA+OF=![]() ��
��
���PAE�����ֵ��S��PAE=S��PAF+S��AEF=![]() ��
��![]() ����
����![]() +
+![]() ��=
��=![]() ��
��
������������P��![]() ��
��![]() ��ʱ����PAE��������������Ϊ
��ʱ����PAE��������������Ϊ![]() ��
��


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ����λ��m�����m����������������ƽ���ͣ���ô�������λ��mΪ��ƽ������������m��a2+b2��a��bΪ������������A��m����ab�����磺29��22+52��29����һ����ƽ������������A��29����2��5��10��
��1���ж�25�Ƿ��ǡ�ƽ�������������ǣ������A��25����ֵ�������ǣ���˵�����ɣ�
��2����k��һ����ƽ������������A��k����![]() ����k��ֵ��
����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�����Ծ�����ɵ�Ӱ�죬ij�����ֱ���һ�߳��к����߳��е�־Ը�������ѡȡ��50�˲μ�LES���ԣ�����־Ը�ߵĴ�����������LES�÷֣����Ե÷ֽ��������������ͷ�����������Ϣ���£�
һ�����߳���־Ը�ߵ÷�ͳ�Ʊ�
���� | ��λ�� | ƽ���� |
һ�߳��� | a | 17.6 |
���߳��� | 14 | 17.2 |
ע��һ�߳�����14��x��20�еĵ÷��ǣ�15��15��16��17��17��17��17��18��18��20��
����������Ϣ������������⣺
��1������a��ֵΪ����������
��2���÷�Խ�ͷ�ӳ������ܵľ���ѹ��ԽС������Խ��ǰ������ε����У�һ�߳��е�־Ը�����߳��е�־Ը���ҵĵ÷־�Ϊ15�֣����жϼס����ڸ��Գ���ѡȡ��־Ը���е÷�����˭����ǰ����˵�����ɣ�
��3������÷ֳ���ƽ��������Ҫ����������Ԥ�������һ�߳���ȫ��2000��־Ը�����ж�������Ҫ����������Ԥ��
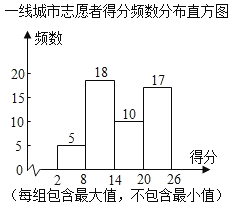
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Уͬ��ȫ���ܵ�ȫ���Ĺ㷺��ע������ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ���������ͼ�����в�������ͳ��ͼ���������ͳ��ͼ�����ṩ����Ϣ����������⣺
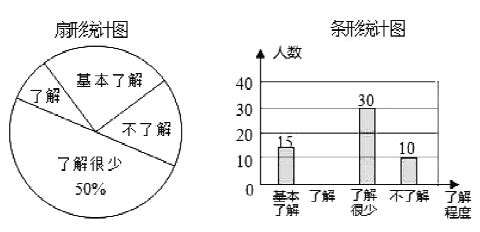
��1�������ʾ������ѧ���������������ˣ�����ͳ��ͼ�С��˽⡱��������Ӧ���ε�Բ�Ľ�Ϊ���������ȣ�����ȫ����ͳ��ͼ��
��2��������ѧ����ѧ��![]() �ˣ���������������������Ƹ���ѧѧ���ж�У��ȫ֪ʶ�ﵽ���˽⡱�͡������˽⡱�̶ȵ�������Ϊ���������ˣ�
�ˣ���������������������Ƹ���ѧѧ���ж�У��ȫ֪ʶ�ﵽ���˽⡱�͡������˽⡱�̶ȵ�������Ϊ���������ˣ�
��3�����Ӷ�У��ȫ֪ʶ�ﵽ���˽⡱�̶ȵ�![]() ��Ů��
����![]() ��
��![]() ������
������![]() �зֱ������ȡ
�зֱ������ȡ![]() �˲μ�У��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽Ů��
�˲μ�У��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽Ů��![]() �ĸ��ʣ�
�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
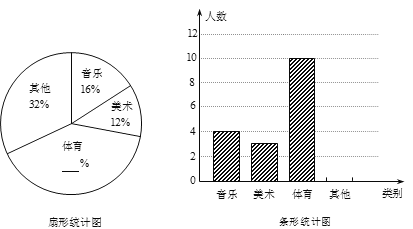
����Ŀ����ͼ��Ϊ�˽�ѧ���Ŀ������������ij��ѧ��ȫУ��Χ�������ȡ����ѧ�������ʾ����飮 �ʾ�����ѧ��ѡ����ϲ���Ŀ����������ࣨÿ��ֻѡһ�ࣩ��ѡ���������ࡢ�����ࡢ�����༰���������࣬��������ݻ��Ƴ�����ͳ��ͼ������ͳ��ͼ����ͼ��ʾ����
��1������˴��ʾ�����ѧ���������ˣ�
��2�����������������ͼ������ͼ����д������ͼ��ȱʧ�����ݣ���������ͼ����������
��3�����ʾ������У�С�ź�С���ֱ�ѡ����������������࣬��ʦҪ��ѡ����������������ѧ���зֱ��ȡһ��ѧ���μӻ����ѡ����������ĸ�ѧ��Ϊ�š�A1��A2��A3��ѡ��������3��ѧ��Ϊ����B1��B2�����б�����״ͼ�ķ�����С�ź�С��ǡ�ö���ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���BAC=��BDC��
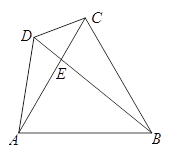
��1����֤����ADE�ס�CEB��
��2����֪��ABC�ǵȱ������Σ���֤��
�� ![]() ��
��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
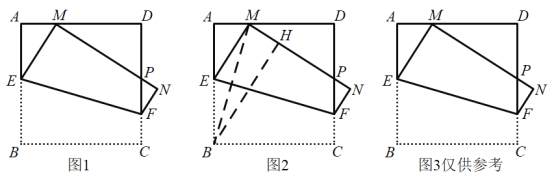
����Ŀ����ͼ1���ڱ߳�Ϊ1��������ABCD�У�����E��F�ֱ��ڱ�AB��CD�ϣ���������ABCD��ֱ��EF�۵���ʹ��B�Ķ�Ӧ��Mʼ�����ڱ�AD��(��M�����A��D�غ�)����C���ڵ�N����MN��CD���ڵ�P����BE��x��
(1)��AM��![]() ʱ����x��ֵ��
ʱ����x��ֵ��
(2)��ͼ2������BM����B����BH��MN������ΪH����֤��BM����ABH�Ľ�ƽ���ߣ�
(3)���ŵ�M�ڱ�AD��λ�õı仯����PDM���ܳ��Ƿ����仯����仯����˵�����ɣ��粻�䣬������ö�ֵ��
(4)���ı���BEFC�����ΪS����S��x֮��ĺ�������ʽ�������S����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ֳ�����ƽ��ͼ��ͼ��ʾ��C��E��A��ͬһֱ������D��E��B��ͬһֱ���������A����E���ľ���Ϊ80 m��C����D���ľ���Ϊ34 m����C��90������ABE��90������BAE��30��.( ![]() ��1.4��
��1.4�� ![]() ��1.7)
��1.7)
(1)����תľ��E��������B���ľ�����
(2)������D��������B���ľ���(�����������)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������C����O��һ�㣨���A��B���غϣ�������C��ֱ��PQ��ʹ�á�ACQ����ABC��
��1����֤��ֱ��PQ����O�����ߣ�
��2������A��AD��PQ�ڵ�D������O�ڵ�E������O�İ뾶Ϊ2��sin��DAC��![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com