
【题目】如图,四边形ABCD中,∠BAC=∠BDC,
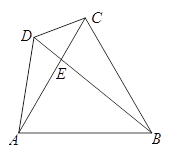
(1)求证:△ADE∽△CEB;
(2)已知△ABC是等边三角形,求证:
① ![]() ;
;
② ![]() .
.
【答案】(1)证明见解析;(2)①证明见解析;②证明见解析
【解析】
(1)证明△BEA∽△DEC,从而得到![]() ,再结合∠AED=∠BEC即可证明△ADE∽△BCE;
,再结合∠AED=∠BEC即可证明△ADE∽△BCE;
(2)①利用等边三角形的性质得到∠ACB=∠BDC,结合∠DBC=∠DBC得到△BEC∽△BCD,根据相似的性质即可得到结果;
②在DB上取点F,使DF=DC,证明△CDF是等边三角形,再证明△DCA≌△FCB,则有AD=BF,继而得到结论.
解:(1)证明:∵∠BAC=∠BDC,∠BEA =∠DEC
∴△BEA∽△DEC
∴ ![]() ,
,
即 ![]()
又∵∠AED=∠BEC
∴△ADE∽△BCE;
(2)证明:①∵△ABC是等边三角形
∴∠ACB=∠BAC=![]()
∵∠BAC=∠BDC
∴∠ACB=∠BDC=![]()
又∵∠DBC=∠DBC
∴△BEC∽△BCD
∴![]()
∴![]()
②在DB上取点F,使DF=DC
∵∠BDC=∠ACB= ![]()
∴△CDF是等边三角形
∴CD=CF,∠DCF= ![]()
∴∠DCF-∠ACF=∠ACB-∠ACF
∴∠DCA=∠FCB
由△ABC是等边三角形得:AC=BC
∴△DCA≌△FCB
∴AD=BF
∴BD=DF+BF=CD+AD.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校九年级有 ![]() 名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个不完整的统计图.请根据相关信息,解答下列问题:
名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个不完整的统计图.请根据相关信息,解答下列问题:
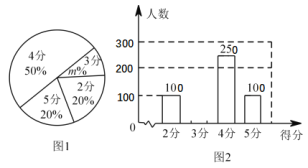
(1)本次参加跳绳测试的学生人数为 ,图 ![]() 中
中 ![]() 的值为 ;
的值为 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校九年级跳绳测试中得 ![]() 分的学生约有多少人?
分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 铀交于
铀交于![]() ,与
,与![]() 轴交于
轴交于![]() 抛物线的顶点为
抛物线的顶点为![]() 直线
直线![]() 过
过![]() 交
交![]() 轴于
轴于![]() .
.
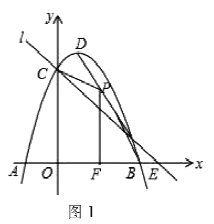
(1)写出![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(2)![]() 是线段
是线段![]() 上的动点(不与
上的动点(不与![]() 重合),
重合),![]() 轴于
轴于![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的两数关系式,并求
之间的两数关系式,并求![]() 的最大值;
的最大值;
(3)点![]() 在
在![]() 轴的正半轴上运动,过
轴的正半轴上运动,过![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于
于![]() 交抛物线于
交抛物线于![]() 连接
连接![]() ,将
,将![]() 沿
沿![]() 翻转,
翻转,![]() 的对应点为
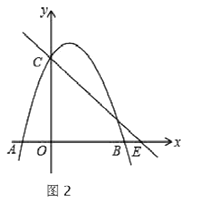
的对应点为![]() .在图2中探究:是否存在点
.在图2中探究:是否存在点![]() ;使得
;使得![]() 恰好落在
恰好落在![]() 轴?若存在,请求出
轴?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
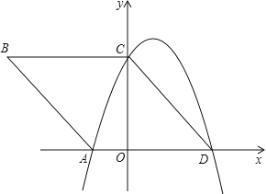
【题目】如图,在平面直角坐标系xOy中,四边形ABCD是边长为5的菱形,顶点A.C.D均在坐标轴上,sinB=![]() .
.
(1)求过A,C,D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1>y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A,E两点之间的一个动点,且直线PE交x轴于点F,问:当P点在何处时,△PAE的面积最大?并求出面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.
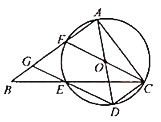
(1)求证:四边形DCFG是平行四边形;(2)当BE=4,CD=![]() AB时,求⊙O的直径长.
AB时,求⊙O的直径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
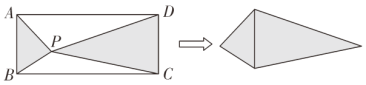
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,P是矩形
,P是矩形![]() 内一点,沿
内一点,沿![]() 、
、![]() 、
、![]() 、
、![]() 把这个矩形剪开,然后把两个阴影三角形拼成一个四边形,则这个四边形的面积为_________;这个四边形周长的最小值为________.
把这个矩形剪开,然后把两个阴影三角形拼成一个四边形,则这个四边形的面积为_________;这个四边形周长的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
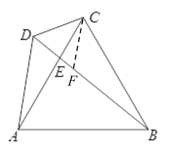
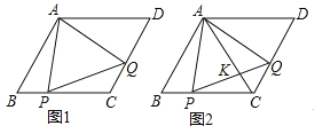
【题目】已知:菱形ABCD,AB=4m,∠B=60°,点P、Q分别从点B、C同时出发,沿线段BC、CD以1m/s的速度向终点C、D运动,运动时间为t秒.
(1)如图1,连接AP、AQ、PQ,试判断△APQ的形状,并说明理由
(2)如图2,当t=1.5秒时,连接AC,与PQ相交于点K.求AK的长.
(3)如图3,连接AC交BD于点O,当P、Q分别运动到点C、D时,将∠APQ沿射线CA方向平移,使点P与点O重合,然后以点O为旋转中心将∠APQ旋转一定的角度,使角的两边分别于CD、AD交于S、K点,再以OS为一边在∠SOC内作∠SOT,使∠SOT=∠BDC,OT边交BC的延长线于点T,若BT=4.8,求AK的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系,相似比为1:3,∠ACB=∠CED=90°,A、C、E是x轴正半轴上的点,B、D是第一象限的点,BC=2,则点D的坐标是( )
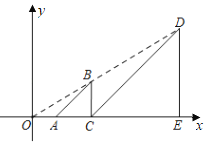
A.(9,6)B.(8,6)C.(6,9)D.(6,8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com