
【题目】已知:菱形ABCD,AB=4m,∠B=60°,点P、Q分别从点B、C同时出发,沿线段BC、CD以1m/s的速度向终点C、D运动,运动时间为t秒.
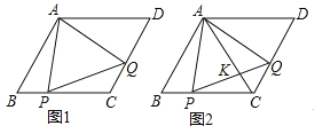
(1)如图1,连接AP、AQ、PQ,试判断△APQ的形状,并说明理由
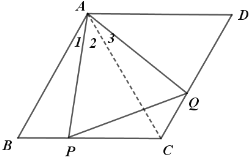
(2)如图2,当t=1.5秒时,连接AC,与PQ相交于点K.求AK的长.
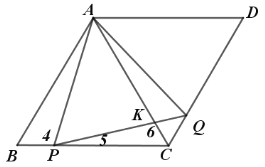
(3)如图3,连接AC交BD于点O,当P、Q分别运动到点C、D时,将∠APQ沿射线CA方向平移,使点P与点O重合,然后以点O为旋转中心将∠APQ旋转一定的角度,使角的两边分别于CD、AD交于S、K点,再以OS为一边在∠SOC内作∠SOT,使∠SOT=∠BDC,OT边交BC的延长线于点T,若BT=4.8,求AK的长.

【答案】(1)等边三角形,见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图1,连接AC,根据菱形的性质证明△ABC和△ACD是等边三角形,得∠B=∠ACQ,AB=AC,由BP=CQ,证明△ABP≌△ACQ,得AP=AQ及∠PAQ=60°,所以△APQ为等边三角形;
(2)由(1)△APQ是等边三角形,由∠4=∠ 6,∠B=∠ACB,得△ABP∽△ PCK,则![]() ,代入数值进行计算,即可得到答案;
,代入数值进行计算,即可得到答案;
(3)由题意先证明△DOS∽△BTO,利用相似三角形的性质,求出DS的长度,然后△AOK∽△ CSO,即可求出AK的长度.
解:(1)△APQ是等边三角形
证明:连接AC
∵菱形ABCD
∴AB=BC
∵∠B=60°
∴△ABC是等边三角形
∴AB=AC,①
∵P、Q分别从点B、C同时出发,且速度相同
∴BP=CQ,②
∵菱形ABCD
∴![]() 120°=60°
120°=60°
∴∠ACQ=∠B③
由①②③得△ABP≌△ACQ
∴AP=AQ ,∠1=∠3,
∵∠1+∠2=∠BAC=![]() 120°=60°
120°=60°
∴∠1+∠3=60°=∠PAQ
∴△APQ是等边三角形
(2)由(1)得△APQ是等边三角形
∴∠APQ=60°
∴∠4+∠5=120°
∵∠ACB=60°
∴∠5+∠6=120°
∴∠4=∠ 6,
∵∠B=∠ACB=60°,
∴△ABP∽△ PCK,
∴![]() ,
,
∵当t=1.5秒时,BP=1.5,
∴CP=4![]() 1.5=2.5,
1.5=2.5,
∴![]()
∴![]() ,
,
∴![]() ;
;
(3) ∵菱形ABCD
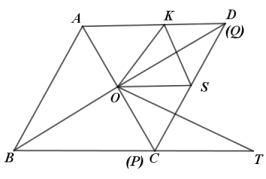
∴∠BDC=∠DBC=![]()
∵∠SOT=∠BDC
可证△DOS∽△BTO
∴![]()
∵BC=4 ,∠BDC=∠DBC=30°
∴CO=AO=2 ,BO=DO=![]()
∴![]()
∴DS=2.5
∴CS=4![]() 2.5=1.5
2.5=1.5
∵∠DAC=∠KOS=∠ACD
可证∴△AOK∽△ CSO
∴![]()
∴![]()
∴![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】某通讯经营店销售![]() ,
,![]() 两种品牌儿童手机,今年进货和销售价格如下表:
两种品牌儿童手机,今年进货和销售价格如下表:
|
| |
进货价格(元/只) | 1000 | 1100 |
销售价格(元/只) |
| 1500 |
已知![]() 型手机去年4月份销售总额为3.6万元,今年经过改造升级后每部销售价比去年增加400元.今年4月份
型手机去年4月份销售总额为3.6万元,今年经过改造升级后每部销售价比去年增加400元.今年4月份![]() 型手机的销售数量与去年4月份相同,而销售总额为5.4万元.
型手机的销售数量与去年4月份相同,而销售总额为5.4万元.
(1)求今年4月份![]() 型手机的销售价是多少元?
型手机的销售价是多少元?
(2)该店计划6月份再进一批![]() 型和
型和![]() 型手机共50部且
型手机共50部且![]() 型手机数量不超过
型手机数量不超过![]() 型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?
型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在扇形![]() 中,
中,![]() ,半径
,半径![]() ,点P为
,点P为![]() 上任一点(不与A、O重合).
上任一点(不与A、O重合).
(1)如图①,Q是![]() 上一点,若
上一点,若![]() ,求证:
,求证:![]() .
.
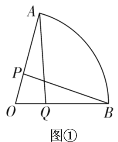
(2)如图②,将扇形沿![]() 折叠,得到O的对称点
折叠,得到O的对称点![]() .
.
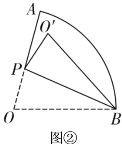
①若点![]() 落在
落在![]() 上,求
上,求![]() 的长;
的长;
②当![]() 与扇形
与扇形![]() 所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C,E,A在同一直线上,D,E,B在同一直线上,测得A处与E处的距离为80 m,C处与D处的距离为34 m,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王芳同学到文具店购买中性笔和笔记本,中性笔每支1元,笔记本每本3元,王芳同学现有10元钱,则可供她选择的购买方案的个数为(两样都买,余下的钱少于1元)( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
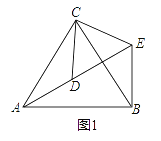
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
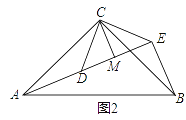
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
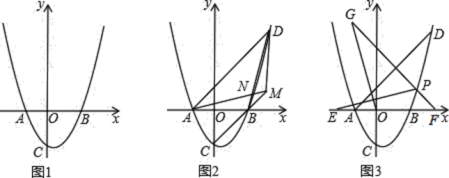
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴负半轴于点
轴负半轴于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,且
,且![]() .
.
(1)如图1,求![]() 的值;
的值;
(2)如图![]() ,
,![]() 是第一象限抛物线上的点,连
是第一象限抛物线上的点,连![]() ,过点
,过点![]() 作
作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标以及
的坐标以及![]() 的值;
的值;
(3)如图3,在(2)的条件下,连接![]() ,
,![]() 是第一象限抛物线上的点(点
是第一象限抛物线上的点(点![]() 与点
与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com