
【题目】某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
【答案】(1)A款保温杯的售价为30元,B款保温杯的售价为40元;(2)进货80个A款保温杯,40个B款保温杯,利润最大,为1440元.
【解析】
(1)设:A款保温杯的售价为x元,B款保温杯的售价为(x+10)元;利用数量相等列方程求解即可;(2)设进货A款保温杯m个,B款保温杯(120-m)个,总利润为w,根据题意得出函数关系式,同时列出不等式组得到m的范围,再利用一次函数的性质得到答案.
(1)设:A款保温杯的售价为x元,B款保温杯的售价为(x+10)元;
![]()
解得x=30,经检验,x=30是原方程的根;
因此A款保温杯的售价为30元,B款保温杯的售价为40元;
(2)由题意得:B款保温杯的售价为40×(1-10%)=36元;
设进货A款保温杯m个,B款保温杯(120-m)个,总利润为w;
w=![]()
![]() ,
,![]()
∵w=![]() 中k=-6<0
中k=-6<0
∴当m最小时,w最大;
∴当m=80时,W最大=1440(元)
答:进货80个A款保温杯,40个B款保温杯,利润最大,为1440元.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
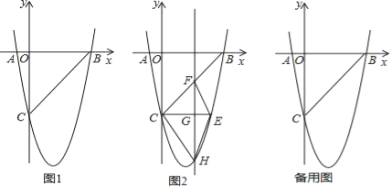
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx-5与x轴交于A(-1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上是否存在点P,Q,使四边形PQKM的周长最小,若没有,说明理由;若有,求出点P,Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
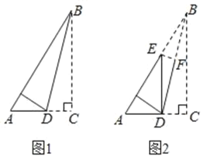
【题目】已知直角三角形纸片的两直角边AC与BC的比为3:4,首先将△ABC如图1所示折叠,使点C落在AB上,折痕为BD,然后将△ABD如图2所示折叠,使点B与点D重合,折痕为EF,则sin∠DEA的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠疫情期间,某医药器材经销商计划同时购进一批甲、乙两种型号的口罩,若购进2箱甲型口罩和1箱乙型口罩,共需要资金2800元;若购进3箱甲型口罩和2箱乙型口罩,共需要资金4600元.
(1)求甲、乙型号口罩每箱的进价为多少元?
(2)该医药器材经销商计划购进甲、乙两种型号的口罩用于销售,预汁用不多于1.8万元且不少于1.74万元的资金购进这两种型号口罩共20箱,请问有几种进货方案?并写出具体的进货方案;
(3)若销售一箱甲型口罩,利润率为40%,乙型口罩的售价为每箱1280元.为了促销,公司决定每售出一箱乙型口罩,返还顾客现金![]() 元,而甲型口罩售价不变,要使(2)中所有方案获利相同,求
元,而甲型口罩售价不变,要使(2)中所有方案获利相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是两座现代化城市,
是两座现代化城市,![]() 是一个古城遗址,
是一个古城遗址,![]() 城在
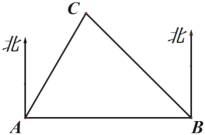
城在![]() 城的北偏东
城的北偏东![]() ,在
,在![]() 城的北偏西
城的北偏西![]() ,
,![]() 城在
城在![]() 城的正东方向,且
城的正东方向,且![]() 城与
城与![]() 城相距120千米,现在
城相距120千米,现在![]() 、
、![]() 两城市修建一条笔直的高速公路.
两城市修建一条笔直的高速公路.
(1)请你计算公路![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)若以![]() 为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路
为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路![]() 会不会穿越这个保护区,并说明理由.
会不会穿越这个保护区,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
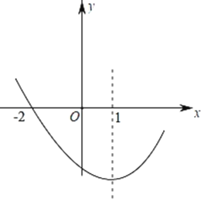
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直x=1线,下列结论中:①abc>0;②若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;③若方程a(x+2)(4﹣x)=﹣2的两根为x1,x2,且x1<x2,则﹣2<x1<x2<4;④(a+c)2>b2;一定正确的是______(填序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
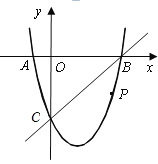
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织1200名师生参加社会实践活动,其中包括25名教师与某公交公司洽谈后得知该公司有A、B型两种客车.每辆A型客车载客54人,租金480元;每辆B型客车载客36人,租金280元.由于每辆车上要求有一名教师,决定租用25辆客车.
设租用A型客车x辆(x为非负整数).
(Ⅰ)根据题意填写下表:
客车类型 | 车辆数(辆) | 载客数(人) | 租金(元) |
A型客车 | x | ||
B型客车 |
|
(Ⅱ)若租车总费用为10800元,怎样安排车辆?
(Ⅲ)采取怎样的租车方案可以使租车总费用最低,最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 左
左![]() 右),交
右),交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
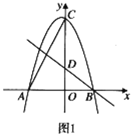
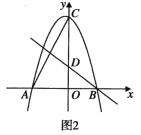
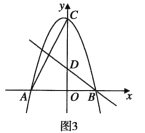
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是第三象限抛物线上的任意一点,设点
是第三象限抛物线上的任意一点,设点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式(不要求写出自变量
的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() 、
、![]() ,当
,当![]() 平分
平分![]() 时,以线段
时,以线段![]() 为边,在
为边,在![]() 上方作等边
上方作等边![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com