
【题目】某学校计划组织1200名师生参加社会实践活动,其中包括25名教师与某公交公司洽谈后得知该公司有A、B型两种客车.每辆A型客车载客54人,租金480元;每辆B型客车载客36人,租金280元.由于每辆车上要求有一名教师,决定租用25辆客车.
设租用A型客车x辆(x为非负整数).
(Ⅰ)根据题意填写下表:
客车类型 | 车辆数(辆) | 载客数(人) | 租金(元) |
A型客车 | x | ||
B型客车 |
|
(Ⅱ)若租车总费用为10800元,怎样安排车辆?
(Ⅲ)采取怎样的租车方案可以使租车总费用最低,最低是多少元?
【答案】(Ⅰ)![]() ,
,![]() ,
,![]() ,
,![]() ;(Ⅱ)安排A型客车19辆,B型客6辆;(Ⅲ)安排A型客车17辆,B型客车8辆,可使租车总费用最低,最低为10400元
;(Ⅱ)安排A型客车19辆,B型客6辆;(Ⅲ)安排A型客车17辆,B型客车8辆,可使租车总费用最低,最低为10400元
【解析】
(Ⅰ)根据载客数=每辆车的载客数乘以车的辆数,租金=每辆车的租金乘以车的辆数即可得到答案
(Ⅱ)将A型客车与B型客车的租金相加即可得到总费用列出方程,解方程即可
(Ⅲ)设租用A型客车x辆,租车总费用为y元,得到函数关系式,根据总人数1200人可列得不等式![]() 求出
求出![]() ,再根据一次函数的增减性即可得到y的最小值.
,再根据一次函数的增减性即可得到y的最小值.
解:(Ⅰ)![]() ,
,![]() ,
,![]() ,
,![]()
(Ⅱ)由租车总费用为10800元,租车总费用可表示为![]() ,可列方程得
,可列方程得![]() .
.
整理得![]() ,
,
解得![]() .
.
∴B型客车为25-19=6(辆).
所以安排A型客车19辆,B型客6辆.
(Ⅲ)设租用A型客车x辆,租车总费用为y元,
则![]() ,其中
,其中![]() ,
,
解得![]() ,
,
∵![]() .
.
∴y随x的增大而增大,
∴当![]() 时,y取得最小值,
时,y取得最小值,![]() (元)
(元)
答:安排A型客车17辆,B型客车8辆,可使租车总费用最低,最低为10400元.


科目:初中数学 来源: 题型:
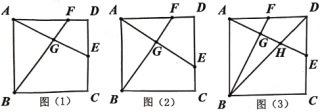
【题目】如图,正方形ABCD的边长为6,E、F分别是边CD、AD上动点,AE和BF交于点G.
(1)如图(1),若E为边CD的中点,AF=2FD,求AG的长.
(2)如图(2),若点F在AD上从A向D运动,点E在DC上从D向C运动,两点同时出发,同时到达各自终点,求在运动过程中,点G运动的路径长.
(3)如图(3),若E、F分别是边CD、AD上的中点,BD与AE交于点H,求∠FBD的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
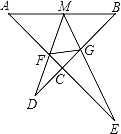
【题目】如图M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于F,ME交BC于G,连接FG,若AB=![]() ,AF=3,则BG=_____,FG=_____.
,AF=3,则BG=_____,FG=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长都为1的小正方形组成的网格中,点B,M均为格点,点A为小正方形边的中点.

(I)线段![]() 的长为____________;
的长为____________;
(Ⅱ)在线段![]() 上存在一点N,使得点N满足
上存在一点N,使得点N满足![]() ,请你借助给定的网格,用无刻度的直尺作出
,请你借助给定的网格,用无刻度的直尺作出![]() ,并简要说明你是怎么找到点N的.(不要求证明)_________________________________________.
,并简要说明你是怎么找到点N的.(不要求证明)_________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设最美恩施,一旅游投资公司拟定在某景区用茶花和月季打造一片人工花海,经市场调查,购买![]() 株茶花与
株茶花与![]() 株月季的费用相同,购买
株月季的费用相同,购买![]() 株茶花与
株茶花与![]() 株月季共需
株月季共需![]() 元.
元.
(1)求茶花和月季的销售单价;
(2)该景区至少需要茶花月季共![]() 株,要求茶花比月季多
株,要求茶花比月季多![]() 株,但订购两种花的总费用不超过
株,但订购两种花的总费用不超过![]() 元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
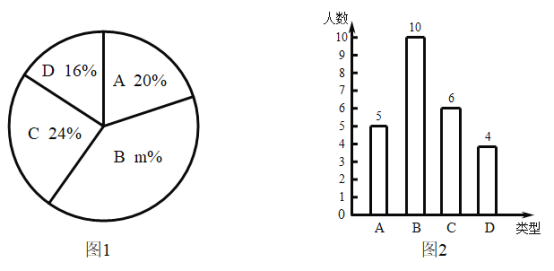
【题目】某校350名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成了图1和图2两个统计图表.
请根据相关信息回答下列问题:
(Ⅰ)此次共随机抽查了_______________名学生每人的植树量;
图①中m的值为_______________________;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计这350名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=2,BC=4.点M1,N1,P1分别在AC,BC,AB上,且四边形M1CN1P1是正方形,点M2,N2,P2分别在P1N1,BN1,BP1上,且四边形M2N1N2P2是正方形,…,点Mn,Nn,Pn分别在Pn-1Nn-1,BNn-1,BPn-1上,且四边形MnNn-1NnPn是正方形,则线段BN2020的长度是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com