
【题目】某校350名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成了图1和图2两个统计图表.
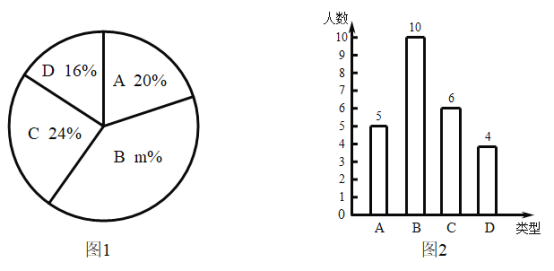
请根据相关信息回答下列问题:
(Ⅰ)此次共随机抽查了_______________名学生每人的植树量;
图①中m的值为_______________________;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计这350名学生共植树多少棵?
【答案】(Ⅰ)25,40;(Ⅱ)平均数是5.36,众数是5,中位数是5;(Ⅲ)1876
【解析】
(Ⅰ)根据条形统计图与扇形统计图的信息计算即可得到答案;
(Ⅱ)根据平均数、众数和中位数的定义求解即可得到答案;
(Ⅲ)根据样本植树的平均数乘以总人数即可得到答案;
解:(Ⅰ)根据条形统计图,得到调查总人数为:5+10+6+4=25(名),
根据扇形统计图得到m=100-20-16-24=40;
故答案为:25,40;
(Ⅱ)观察条形统计图,∵![]() .
.
∴这组数据的平均数是5.36.
∵在这组样本数据中,5出现了10次,出现的次数最多,
∴这组样本数据的众数是5.
将这组样本数据按照由小到大的顺序排列,其中处于中间位置的数是5,
∴这组样本数据的中位数是5.
(Ⅲ)∵样本数据的平均数是5.36
∴可以用样本平均数估计总体平均数为5.36
∵![]() .
.
答:这350人约共植树1876棵.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】新冠疫情期间,某医药器材经销商计划同时购进一批甲、乙两种型号的口罩,若购进2箱甲型口罩和1箱乙型口罩,共需要资金2800元;若购进3箱甲型口罩和2箱乙型口罩,共需要资金4600元.
(1)求甲、乙型号口罩每箱的进价为多少元?
(2)该医药器材经销商计划购进甲、乙两种型号的口罩用于销售,预汁用不多于1.8万元且不少于1.74万元的资金购进这两种型号口罩共20箱,请问有几种进货方案?并写出具体的进货方案;
(3)若销售一箱甲型口罩,利润率为40%,乙型口罩的售价为每箱1280元.为了促销,公司决定每售出一箱乙型口罩,返还顾客现金![]() 元,而甲型口罩售价不变,要使(2)中所有方案获利相同,求
元,而甲型口罩售价不变,要使(2)中所有方案获利相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织1200名师生参加社会实践活动,其中包括25名教师与某公交公司洽谈后得知该公司有A、B型两种客车.每辆A型客车载客54人,租金480元;每辆B型客车载客36人,租金280元.由于每辆车上要求有一名教师,决定租用25辆客车.
设租用A型客车x辆(x为非负整数).
(Ⅰ)根据题意填写下表:
客车类型 | 车辆数(辆) | 载客数(人) | 租金(元) |
A型客车 | x | ||
B型客车 |
|
(Ⅱ)若租车总费用为10800元,怎样安排车辆?
(Ⅲ)采取怎样的租车方案可以使租车总费用最低,最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好新型肺炎疫情防控,某社区开展新型肺炎疫情排查与宣传教育志愿服务活动,组织社区20名志愿者随机平均分配在4个院落门甲、乙、丙、丁处值守,并对进出人员进行测温度、劝导佩戴口罩、正确投放生活垃圾等服务.
(1)志愿者小明被分配到甲处服务是( )事件;
A.不可能事件 B.可能事件 C.必然事件 D.无法确定
(2)请用列表或树状图的方法,求出志愿者小明和小红被随机分配到同一处服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,抛物线
,抛物线![]() 图象经过
图象经过![]() 三点.
三点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上的一个动点,作
下方的抛物线上的一个动点,作![]() 于点
于点![]() ,当
,当![]() 的值最大时,求此时点
的值最大时,求此时点![]() 的坐标及
的坐标及![]() 的最大值.
的最大值.
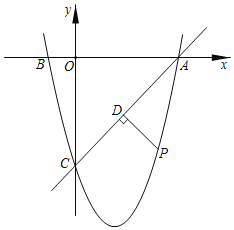
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 左
左![]() 右),交
右),交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
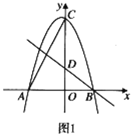
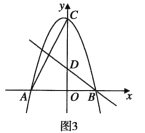
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是第三象限抛物线上的任意一点,设点
是第三象限抛物线上的任意一点,设点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式(不要求写出自变量
的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
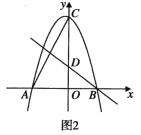
(3)在(2)的条件下,连接![]() 、
、![]() ,当
,当![]() 平分
平分![]() 时,以线段
时,以线段![]() 为边,在
为边,在![]() 上方作等边
上方作等边![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
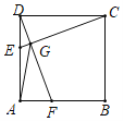
【题目】如图,边长为2的正方形ABCD中,点E、F分别在AD、AB上(点E不与点D重合),DE=AF,DF、CE交于点G,则AG的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究证明)(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:
如图①,在矩形ABCD中,EF⊥GH,EF分别交AD、BC于点E、F,GH分别交AB、DC于点G、H,求证:![]() ;
;
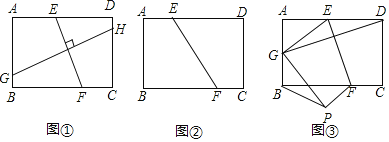
(结论应用)(2)如图②,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3.求折痕EF的长;
(拓展运用)(3)如图③,将矩形ABCD沿EF折叠.使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG,若AB=2,BC=3,EF=![]() ,请求BP的长.
,请求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com