
ЁОЬтФПЁПЃЈЬНОПжЄУїЃЉЃЈ1ЃЉФГАрЪ§бЇПЮЬтбЇЯАаЁзщЖдОиаЮФкСНЬѕЛЅЯрДЙжБЕФЯпЖЮгыОиаЮСНСкБпЕФЪ§СПЙиЯЕНјааЬНОПЃЌЬсГіЯТСаЮЪЬтЃЌЧыФуИјГіжЄУїЃК
ШчЭМЂйЃЌдкОиаЮABCDжаЃЌEFЁЭGHЃЌEFЗжБ№НЛADЁЂBCгкЕуEЁЂFЃЌGHЗжБ№НЛABЁЂDCгкЕуGЁЂHЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
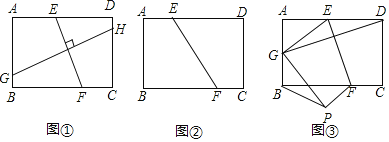
ЃЈНсТлгІгУЃЉЃЈ2ЃЉШчЭМЂкЃЌНЋОиаЮABCDбиEFелЕўЃЌЪЙЕУЕуBКЭЕуDжиКЯЃЌШєABЃН2ЃЌBCЃН3ЃЎЧѓелКлEFЕФГЄЃЛ
ЃЈЭиеЙдЫгУЃЉЃЈ3ЃЉШчЭМЂлЃЌНЋОиаЮABCDбиEFелЕўЃЎЪЙЕУЕуDТфдкABБпЩЯЕФЕуGДІЃЌЕуCТфдкЕуPДІЃЌЕУЕНЫФБпаЮEFPGЃЌШєABЃН2ЃЌBCЃН3ЃЌEFЃН![]() ЃЌЧыЧѓBPЕФГЄЃЎ
ЃЌЧыЧѓBPЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉEFЃН![]() ЃЛЃЈ3ЃЉBPЃН
ЃЛЃЈ3ЃЉBPЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуAзїAPЁЮEFЃЌНЛBCгкPЃЌЙ§ЕуBзїBQЁЮGHЃЌНЛCDгкQЃЌШчЭМ1ЃЌвзжЄAP=EFЃЌGH=BQЃЌЁїABPЁзЁїBCQЃЌШЛКѓдЫгУЯрЫЦШ§НЧаЮЕФаджЪОЭПЩНтОіЮЪЬтЃЛ
(2)СЌНгBDЃЌИљОнОиаЮЕФаджЪЕУГіBDЕФГЄЃЌдйИљОнНсТлЃЈ1ЃЉЕУГі![]() ЃЌНјЖјПЩЧѓГіEFЕФГЄ.
ЃЌНјЖјПЩЧѓГіEFЕФГЄ.
ЃЈ3ЃЉЙ§ЕуFзїFHЁЭEGгкHЃЌЙ§ЕуPзїPJЁЭBFгкJЃЎИљОнОиаЮЕФаджЪЕУЕНADЁЂCDЕФГЄЃЌгЩНсТлЃЈ1ЃЉПЩЕУГіDGЕФГЄЃЌдйгЩЙДЙЩЖЈРэЕУГіAGЕФГЄЃЌШЛКѓИљОнЗелЕФаджЪНсКЯЙДЙЩЖЈРэЕУГіЫФБпаЮHGPFЪЧОиаЮЃЌНјЖјЕУГіFHЕФГЄЖШЃЌзюКѓИљОнЯрЫЦШ§НЧаЮЕУГіBJЁЂPJЕФГЄЖШОЭПЩвдЕУГіBPЕФГЄЖШ.
ЃЈ1ЃЉШчЭМЂйЃЌЙ§ЕуAзїAPЁЮEFЃЌНЛBCгкPЃЌЙ§ЕуBзїBQЁЮGHЃЌНЛCDгкQЃЌBQНЛAPгкTЃЎ
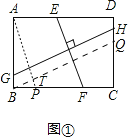
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрABЁЮDCЃЌADЁЮBCЃЎ
ЁрЫФБпаЮAEFPЁЂЫФБпаЮBGHQЖМЪЧЦНааЫФБпаЮЃЌ
ЁрAPЃНEFЃЌGHЃНBQЃЎ
гжЁпGHЁЭEFЃЌ
ЁрAPЁЭBQЃЌ
ЁрЁЯBAT+ЁЯABTЃН90ЁуЃЎ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯABPЃНЁЯCЃН90ЁуЃЌADЃНBCЃЌ
ЁрЁЯABT+ЁЯCBQЃН90ЁуЃЌ
ЁрЁЯBAPЃНЁЯCBQЃЌ
ЁрЁїABPЁзЁїBCQЃЌ
Ёр![]() ,
,
Ёр![]() .
.
ЃЈ2ЃЉШчЭМЂкжаЃЌСЌНгBDЃЎ
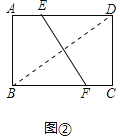
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯCЃН90ЁуЃЌABЃНCDЃН2ЃЌ
ЁрBDЃН![]() ,
,
ЁпDЃЌBЙигкEFЖдГЦЃЌ
ЁрBDЁЭEFЃЌ
Ёр![]() ,
,
Ёр![]() ,
,
ЁрEFЃН![]() .
.
ЃЈ3ЃЉШчЭМЂлжаЃЌЙ§ЕуFзїFHЁЭEGгкHЃЌЙ§ЕуPзїPJЁЭBFгкJЃЎ
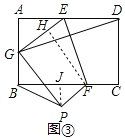
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрABЃНCDЃН2ЃЌADЃНBCЃН3ЃЌЁЯAЃН90ЁуЃЌ
Ёр![]() =
= ![]() ,
,
ЁрDGЃН![]() ЃЌ
ЃЌ
ЁрAGЃН![]() ЃН1ЃЌ
ЃН1ЃЌ
гЩЗелПЩжЊЃКEDЃНEGЃЌЩшEDЃНEGЃНxЃЌ
дкRtЁїAEGжаЃЌЁпEG2ЃНAE2+AG2ЃЌ
Ёрx2ЃНAG2+AE2ЃЌ
Ёрx2ЃНЃЈ3ЉxЃЉ2+1ЃЌ
ЁрxЃН![]() ЃЌ
ЃЌ
ЁрDEЃНEGЃН![]() ЃЌ
ЃЌ
ЁпFHЁЭEGЃЌ
ЁрЁЯFHGЃНЁЯHGPЃНЁЯGPFЃН90ЁуЃЌ
ЁрЫФБпаЮHGPFЪЧОиаЮЃЌ
ЁрFHЃНPGЃНCDЃН2ЃЌ
ЁрEHЃН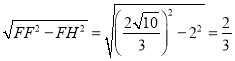 ЃЌ
ЃЌ
ЁрGHЃНFPЃНCFЃНEGЉEHЃН![]() Љ
Љ![]() ЃН1ЃЌ
ЃН1ЃЌ
ЁпPFЁЮEGЃЌEAЁЮFBЃЌ
ЁрЁЯAEGЃНЁЯJPFЃЌ
ЁпЁЯAЃНЁЯFJPЃН90ЁуЃЌ
ЁрЁїAEGЁзЁїJFPЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр ЃЌ
ЃЌ
ЁрFJЃН![]() ЃЌPJЃН
ЃЌPJЃН![]() ЃЌ
ЃЌ
ЁрBJЃНBCЉFJЉCFЃН3Љ![]() Љ1ЃН
Љ1ЃН![]() ЃЌ
ЃЌ
дкRtЁїBJPжаЃЌBPЃН ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃ350УћбЇЩњВЮМгжВЪїЛюЖЏЃЌвЊЧѓУПШЫжВ4~7ПУЃЌЛюЖЏНсЪјКѓЫцЛњГщВщСЫШєИЩУћбЇЩњУПШЫЕФжВЪїСПЃЌВЂЗжЮЊЫФжжРраЭЃЌAЃК4ПУЃЛBЃК5ПУЃЛCЃК6ПУЃЛDЃК7ПУЃЌНЋИїРрЕФШЫЪ§ЛцжЦГЩСЫЭМ1КЭЭМ2СНИіЭГМЦЭМБэ.
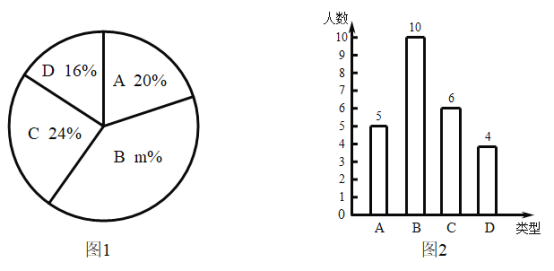
ЧыИљОнЯрЙиаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈЂёЃЉДЫДЮЙВЫцЛњГщВщСЫ_______________УћбЇЩњУПШЫЕФжВЪїСПЃЛ
ЭМЂйжаmЕФжЕЮЊ_______________________ЃЛ
ЃЈЂђЃЉЧѓЭГМЦЕФетзщЪ§ОнЕФЦНОљЪ§ЁЂжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈЂѓЃЉИљОнбљБОЪ§ОнЃЌЙРМЦет350УћбЇЩњЙВжВЪїЖрЩйПУЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН2ЃЌBCЃН4ЃЎЕуM1ЃЌN1ЃЌP1ЗжБ№дкACЃЌBCЃЌABЩЯЃЌЧвЫФБпаЮM1CN1P1ЪЧе§ЗНаЮЃЌЕуM2ЃЌN2ЃЌP2ЗжБ№дкP1N1ЃЌBN1ЃЌBP1ЩЯЃЌЧвЫФБпаЮM2N1N2P2ЪЧе§ЗНаЮЃЌЁЃЌЕуMnЃЌNnЃЌPnЗжБ№дкPnЃ1NnЃ1ЃЌBNnЃ1ЃЌBPnЃ1ЩЯЃЌЧвЫФБпаЮMnNnЃ1NnPnЪЧе§ЗНаЮЃЌдђЯпЖЮBN2020ЕФГЄЖШЪЧ__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃПЊеЙбабЇТУааЛюЖЏЃЌзМБИШЅЕФбабЇЛљЕигаAЃЈЧњИЗЃЉЁЂBЃЈСКЩНЃЉЁЂCЃЈуыЩЯЃЉЃЌDЃЈуєЫЎЃЉЃЌУПЮЛбЇЩњжЛФмбЁШЅвЛИіЕиЗНЃЌЭѕРЯЪІЖдБОШЋЬхЭЌбЇбЁШЁЕФбабЇЛљЕиЧщПіНјааЕїВщЭГМЦЃЌЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЈШчЭМЫљЪОЃЉЃЎ
ЃЈ1ЃЉЧѓИУАрЕФзмШыЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉЧѓDЃЈуєЫЎЃЉЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ3ЃЉИУАрАрЮЏ4ШЫжаЃЌ1ШЫбЁШЅЧњИЗЃЌ2ШЫбЁШЅСКЩНЃЌ1ШЫбЁШЅуыЩЯЃЌЭѕРЯЪІвЊДгет4ШЫжаЫцЛњГщШЁ2ШЫСЫНтЫћУЧЖдбабЇЛљЕиЕФПДЗЈЃЌЧыФугУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓЫљГщШЁЕФ2ШЫжаЧЁКУга1ШЫбЁШЅЧњИЗЃЌ1ШЫбЁШЅСКЩНЕФИХТЪЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃзщжЏбЇЩњВЮМгЁАаТЙкЗЮбзЁБЗРвпжЊЪЖОКШќЃЌДгжаГщШЁСЫВПЗжбЇЩњГЩМЈНјааЭГМЦЃЌВЂАДееГЩМЈДгЕЭЕНИпЗжГЩAЃЌBЃЌCЃЌDЃЌEЮхИіаЁзщЃЌЛцжЦЭГМЦЭМШчБэЃЈЮДЭъГЩЃЉЃЌНтД№ЯТСаЮЪЬтЃК
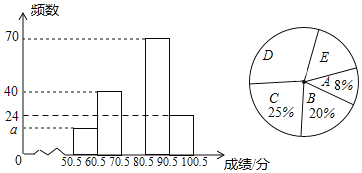
ЃЈ1ЃЉбљБОШнСПЮЊЁЁ ЃЌЦЕЪ§ЗжВМжБЗНЭМжаaЃНЁЁ ЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаEаЁзщЫљЖдгІЕФЩШаЮдВаФНЧЮЊnЁуЃЌЧѓnЕФжЕВЂВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШєГЩМЈдк80ЗжвдЩЯЃЈВЛКЌ80ЗжЃЉЮЊгХауЃЌШЋаЃЙВга3000УћбЇЩњЃЌЙРМЦГЩМЈгХауЕФбЇЩњгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
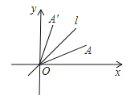
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЯпЖЮOAгыЯпЖЮOAЁфЙигкжБЯпlЃКyЃНxЖдГЦЃЎвбжЊЕуAЕФзјБъЮЊЃЈ2ЃЌ1ЃЉЃЌдђЕуAЁфЕФзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
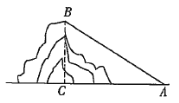
ЁОЬтФПЁПШчЭМЃЌдкСЋЛЈЩНЛЌбЉГЁЛЌбЉЃЌашДгЩННХЯТГЫРТГЕЩЯЩНЃЌРТГЕЫїЕРгыЫЎЦНЯпЫљГЩЕФНЧЮЊ 32ЁуЃЌРТГЕЫйЖШЮЊУПЗжжг 50 УзЃЌДгЩННХЯТA ЕНДяЩНЖЅ B РТГЕашвЊ 16 ЗжжгЃЌдђЩНЕФИпЖШ BC дМЮЊ ____УзЃЎЃЈНсЙћОЋШЗЕН 0.1 УзЃЌВЮПМЪ§ОнЃКsin32ЁуЃН0.5299ЃЌ cos32ЁуЃН0.8480ЃЌtan32ЁуЃН0.6249ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
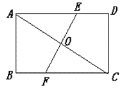
ЁОЬтФПЁПШчЭМЃЌШчЙћНЋОиаЮжНЦЌABCDбиEFелЕўЃЌПЩЪЙЕуAгыЕуCжиКЯЃЌвбжЊABЃН4cmЃЌ AEЃН5 cmЃЌдђEFЕФГЄЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаТЙкЗЮбзвпЧщБЌЗЂжЎКѓЃЌШЋЙњаэЖрЪЁЪаЖдКўББИїЕиНјааСЫдЎжњЃЌЙужнЪаФГвНСЦЖгБИКУвНСЦЗРЛЄЮязЪбИЫйдЎжњЮфККЃЎЕквЛХњвНСЦЖгдБГЫзјИпЬњДгЙужнГіЗЂЃЌ2.5аЁЪБКѓЃЌЕкЖўХњвНСЦЖгдБГЫзјЗЩЛњДгЙужнГіЗЂЃЌСНХњЖгдБИеКУЭЌЪБЕНДяЮфККЃЎвбжЊЙужнЕНЮфККЕФЗЩааОрРыЮЊ800ЧЇУзЃЌИпЬњТЗГЬЮЊЗЩааОрРыЕФ![]() БЖЃЎ
БЖЃЎ
ЃЈ1ЃЉЧѓЙужнЕНЮфККЕФИпЬњТЗГЬЃЛ
ЃЈ2ЃЉШєЗЩЛњЫйЖШгыИпЬњЫйЖШжЎБШЮЊ5ЃК2ЃЌЧѓЗЩЛњКЭИпЬњЕФЫйЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com