
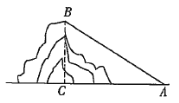
【题目】如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为 32°,缆车速度为每分钟 50 米,从山脚下A 到达山顶 B 缆车需要 16 分钟,则山的高度 BC 约为 ____米.(结果精确到 0.1 米,参考数据:sin32°=0.5299, cos32°=0.8480,tan32°=0.6249)
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 左
左![]() 右),交
右),交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
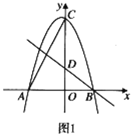
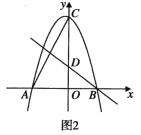
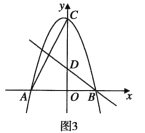
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是第三象限抛物线上的任意一点,设点
是第三象限抛物线上的任意一点,设点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式(不要求写出自变量
的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() 、
、![]() ,当
,当![]() 平分
平分![]() 时,以线段
时,以线段![]() 为边,在
为边,在![]() 上方作等边
上方作等边![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
文文根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是文文的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是__________________;
的自变量x的取值范围是__________________;
(2)下表是y与x的几组对应值:
x | … |
|
|
|
|
| 0 |
| 1 |
| 2 | 3 | … |
y | … |
| 5 |
|
|
| 1 |
|
|
|
|
| … |
则m的值为____________;
(3)如图,在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
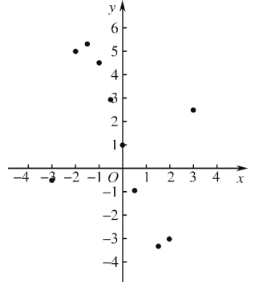
(4)请你根据探究二次函数与一元二次方程关系的经验,结合图象直接写出方程![]() 的正数根约为____________.(结果精确到0.1)
的正数根约为____________.(结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究证明)(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:
如图①,在矩形ABCD中,EF⊥GH,EF分别交AD、BC于点E、F,GH分别交AB、DC于点G、H,求证:![]() ;
;
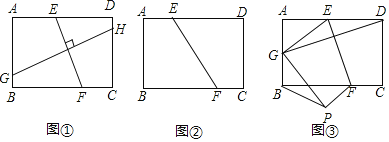
(结论应用)(2)如图②,将矩形ABCD沿EF折叠,使得点B和点D重合,若AB=2,BC=3.求折痕EF的长;
(拓展运用)(3)如图③,将矩形ABCD沿EF折叠.使得点D落在AB边上的点G处,点C落在点P处,得到四边形EFPG,若AB=2,BC=3,EF=![]() ,请求BP的长.
,请求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
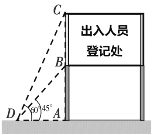
【题目】2020春节期间,为了进一步做好新型冠状病毒感染的肺炎疫情防控工作,防止新型肺炎外传,切断传播途径.项城市市区各入口一些主要路段均设立了检测点,对出入人员进行登记和体温检测。下图为一关口的警示牌,已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求警示牌BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
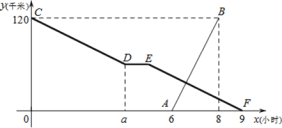
【题目】甲、乙两地相距 120 千米,小张骑自行车从甲地出发匀速驶往乙地,出发 a小时开始休息,1 小时后仍按原速继续行驶.小李比小张晚出发一段时间,骑摩托车从乙地匀速驶往甲地,图中折线 CD-DE-EF,线段 AB 分别表示小张、小李与乙地的距离 y(千米)与小张出发时间 x(小时)之间的函数关系图象.
(1)小李到达甲地后,再经过 小时小张到达乙地;小张骑自行车的速度是 千米/时;
(2)当 a=4 时,求小张与乙地的距离 y乙 与小张出发的时间 x(小时)之间的函数关系式;
(3)若小张恰好在休息期间与小李相遇,请直接写出 a 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 均是
均是![]() 的函数,下表是
的函数,下表是![]() 与
与![]() 的几组对应值.
的几组对应值.

小聪根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,分别对函数
之间的变化规律,分别对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小聪的探究过程,请补充完整:
(1)如图,在同一平面直角坐标系![]() 中,描出上表中各组数值所对应的点
中,描出上表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;

(2)结合画出的函数图象,解决问题:
①当![]() 时,对应的函数值
时,对应的函数值![]() 约为_________;
约为_________;
②写出函数![]() 的一条性质:_________________________;
的一条性质:_________________________;
③当![]() 时,
时,![]() 的取值范围是_________________________.
的取值范围是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
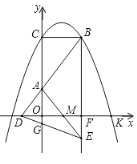
【题目】如图,![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴的正半轴交于点K,过点
轴的正半轴交于点K,过点![]() 作
作![]() 轴交抛物线于另一点B,点
轴交抛物线于另一点B,点![]() 在
在![]() 轴的负半轴上,连结
轴的负半轴上,连结![]() 交
交![]() 轴于点A,若
轴于点A,若![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)当![]() 时,判断点
时,判断点![]() 是否落在抛物线上,并说明理由;
是否落在抛物线上,并说明理由;
(3)过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() 延长
延长![]() 至
至![]() ,使得
,使得![]() 连结
连结![]() 交
交![]() 轴于点
轴于点![]() 连结AE交
连结AE交![]() 轴于点
轴于点![]() 若
若![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 则求出抛物线的解析式.
则求出抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
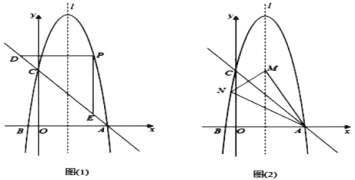
【题目】已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(-1,0),交y轴于点C.
(1)求抛物线的解析式和顶点坐标;
(2)如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴,y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;
(3)如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com