
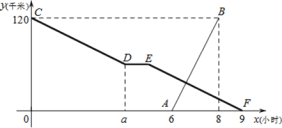
【题目】甲、乙两地相距 120 千米,小张骑自行车从甲地出发匀速驶往乙地,出发 a小时开始休息,1 小时后仍按原速继续行驶.小李比小张晚出发一段时间,骑摩托车从乙地匀速驶往甲地,图中折线 CD-DE-EF,线段 AB 分别表示小张、小李与乙地的距离 y(千米)与小张出发时间 x(小时)之间的函数关系图象.
(1)小李到达甲地后,再经过 小时小张到达乙地;小张骑自行车的速度是 千米/时;
(2)当 a=4 时,求小张与乙地的距离 y乙 与小张出发的时间 x(小时)之间的函数关系式;
(3)若小张恰好在休息期间与小李相遇,请直接写出 a 的取值范围.
【答案】(1)1,15;(2)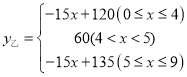 ;(3)
;(3)![]()
【解析】
(1)根据函数图象的横轴计算即可得解;根据速度=路程÷时间,计算即可得解;
(2)利用待定系数法求一次函数解析式求出EF、AB的解析式,然后分小张在小李的前方和小李在小张的前方分别列式计算即可得解;
(3)设小张出发![]() 小时与小李两人相遇,然后列出方程计算并用
小时与小李两人相遇,然后列出方程计算并用![]() 表示出
表示出![]() ,再根据
,再根据![]() 与
与![]() 的差在0到1之间列出不等式组求解即可.
的差在0到1之间列出不等式组求解即可.
(1)9-8=1(小时),小李到达甲地后,再经过1小时小张到达乙地;
![]() (千米/小时),小张骑自行车的速度是15千米/小时;
(千米/小时),小张骑自行车的速度是15千米/小时;
故答案为:1,15;
(2)根据题意得:D(4,60),E(5,60),F(9,0),
设线段EF的函数关系是为![]() ,
,
把E(5,60)和F(9,0)代入得 ,解得
,解得 ,
,
∴![]() ;
;
设线段CD的解析式为![]() ,把D(4,60)代入得:
,把D(4,60)代入得:![]() ,解得
,解得![]() ,
,
∴线段CD的解析式为![]() ,
,
∴当![]() 时,求小张与乙地的距离
时,求小张与乙地的距离![]() 与小张出发的时间
与小张出发的时间![]() (小时)之间的函数关系式为:
(小时)之间的函数关系式为:
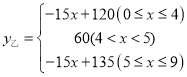 ;
;
(3)设小张出发![]() 小时与小李两人相遇,
小时与小李两人相遇,
小李骑摩托车的速度是:![]() (千米/小时),
(千米/小时),
根据题意得,![]() ,
,
整理得,![]() ,
,
∵小张恰好在休息期间与小李相遇,
∴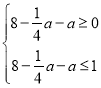 ,
,
解不等式![]() 得:
得:![]() ,
,
解不等式![]() 得:
得:![]() ,
,
∴![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】定义:有三个内角相等的四边形叫三等角四边形.
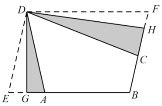
(1)如图,折叠平行四边形纸片![]() ,使顶点
,使顶点![]() ,
,![]() 别落在边
别落在边![]() ,
,![]() 的点
的点![]() ,
,![]() 处,折痕分别为
处,折痕分别为![]() ,
,![]() .求证:四边形
.求证:四边形![]() 是三等角四边形;
是三等角四边形;
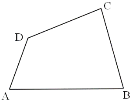
(2)当![]() 时,如图所示,在三等角四边形
时,如图所示,在三等角四边形![]() 中,
中,![]() ,若
,若![]() ,设
,设![]() ,
,![]() ,求y与x的函数关系式,并求出
,求y与x的函数关系式,并求出![]() 的最大值是多少?
的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展研学旅行活动,准备去的研学基地有A(曲阜)、B(梁山)、C(汶上),D(泗水),每位学生只能选去一个地方,王老师对本全体同学选取的研学基地情况进行调查统计,绘制了两幅不完整的统计图(如图所示).
(1)求该班的总入数,并补全条形统计图.
(2)求D(泗水)所在扇形的圆心角度数;
(3)该班班委4人中,1人选去曲阜,2人选去梁山,1人选去汶上,王老师要从这4人中随机抽取2人了解他们对研学基地的看法,请你用列表或画树状图的方法,求所抽取的2人中恰好有1人选去曲阜,1人选去梁山的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
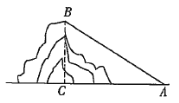
【题目】如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为 32°,缆车速度为每分钟 50 米,从山脚下A 到达山顶 B 缆车需要 16 分钟,则山的高度 BC 约为 ____米.(结果精确到 0.1 米,参考数据:sin32°=0.5299, cos32°=0.8480,tan32°=0.6249)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 的对角线
的对角线![]() 交点
交点![]() ,点
,点![]() 分别为边
分别为边![]() 的中点.有下列四个推断,
的中点.有下列四个推断,
①对于任意四边形![]() ,四边形
,四边形![]() 都是平行四边形;
都是平行四边形;
②若四边形![]() 是平行四边形,则
是平行四边形,则![]() 与
与![]() 交于点
交于点![]() ;
;
③若四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 也是矩形;
也是矩形;
④若四边形![]() 是正方形,则四边形
是正方形,则四边形![]() 也一定是正方形.
也一定是正方形.
所有正确推断的序号是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天,求甲、乙两厂每天能生产口罩多少万只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场打算在年前用30000元购进一批彩灯进行销售,由于进货厂家促销,实际可以以8折的价格购进这批彩灯,结果可以比计划多购进了100盏彩灯.
(1)该商场购进这种彩灯的实际进价为多少元?
(2)该商场打算在实际进价的基础上,每盏灯加价50%的销售,但可能会面临滞销,因此将有20%的彩灯需要降价,以5折出售,该商场要想获利不低于15000元,应至少在购进这种彩灯多少盏?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com