
【题目】定义:有三个内角相等的四边形叫三等角四边形.
(1)如图,折叠平行四边形纸片![]() ,使顶点
,使顶点![]() ,
,![]() 别落在边
别落在边![]() ,
,![]() 的点
的点![]() ,
,![]() 处,折痕分别为
处,折痕分别为![]() ,
,![]() .求证:四边形
.求证:四边形![]() 是三等角四边形;
是三等角四边形;
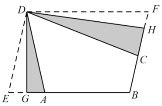
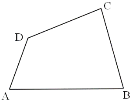
(2)当![]() 时,如图所示,在三等角四边形
时,如图所示,在三等角四边形![]() 中,
中,![]() ,若
,若![]() ,设
,设![]() ,
,![]() ,求y与x的函数关系式,并求出
,求y与x的函数关系式,并求出![]() 的最大值是多少?
的最大值是多少?
科目:初中数学 来源: 题型:
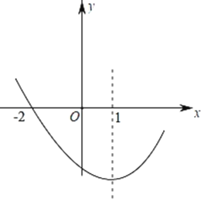
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直x=1线,下列结论中:①abc>0;②若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;③若方程a(x+2)(4﹣x)=﹣2的两根为x1,x2,且x1<x2,则﹣2<x1<x2<4;④(a+c)2>b2;一定正确的是______(填序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好新型肺炎疫情防控,某社区开展新型肺炎疫情排查与宣传教育志愿服务活动,组织社区20名志愿者随机平均分配在4个院落门甲、乙、丙、丁处值守,并对进出人员进行测温度、劝导佩戴口罩、正确投放生活垃圾等服务.
(1)志愿者小明被分配到甲处服务是( )事件;
A.不可能事件 B.可能事件 C.必然事件 D.无法确定
(2)请用列表或树状图的方法,求出志愿者小明和小红被随机分配到同一处服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
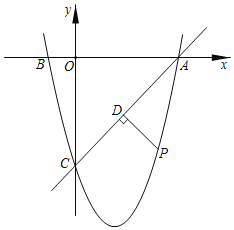
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,抛物线
,抛物线![]() 图象经过
图象经过![]() 三点.
三点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上的一个动点,作
下方的抛物线上的一个动点,作![]() 于点
于点![]() ,当
,当![]() 的值最大时,求此时点
的值最大时,求此时点![]() 的坐标及
的坐标及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 左
左![]() 右),交
右),交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
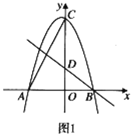
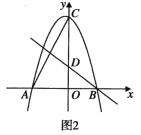
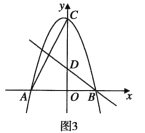
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是第三象限抛物线上的任意一点,设点
是第三象限抛物线上的任意一点,设点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式(不要求写出自变量
的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() 、
、![]() ,当
,当![]() 平分
平分![]() 时,以线段
时,以线段![]() 为边,在
为边,在![]() 上方作等边
上方作等边![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有六张正面分别标有数字﹣2,﹣1,0,1,2,3的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,将该卡片上的数字加1记为b,则函数y=ax2+bx+2的图象过点(1,3)的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD中,点E、F分别在AD、AB上(点E不与点D重合),DE=AF,DF、CE交于点G,则AG的取值范围是( )
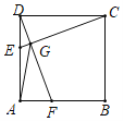
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,在平面直角坐标系xOy中,直线![]() 与y轴交于点C,与x轴交于点B,抛物线
与y轴交于点C,与x轴交于点B,抛物线![]() 经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
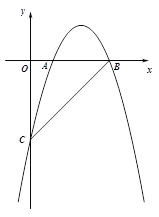


(1)求抛物线的解析式;
(2)点D为线段CB上,点P在对称轴的右侧抛物线上,PD=PB,当tan∠PDB=2,求P点的坐标;
(3)在(2)的条件下,点Q(7,m)在第四象限内,点R在对称轴的右侧抛物线上,若以点P、D、Q、R为顶点的四边形为平行四边形,求点Q、R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
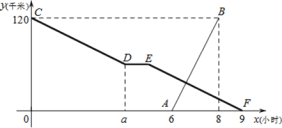
【题目】甲、乙两地相距 120 千米,小张骑自行车从甲地出发匀速驶往乙地,出发 a小时开始休息,1 小时后仍按原速继续行驶.小李比小张晚出发一段时间,骑摩托车从乙地匀速驶往甲地,图中折线 CD-DE-EF,线段 AB 分别表示小张、小李与乙地的距离 y(千米)与小张出发时间 x(小时)之间的函数关系图象.
(1)小李到达甲地后,再经过 小时小张到达乙地;小张骑自行车的速度是 千米/时;
(2)当 a=4 时,求小张与乙地的距离 y乙 与小张出发的时间 x(小时)之间的函数关系式;
(3)若小张恰好在休息期间与小李相遇,请直接写出 a 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com