
【题目】如图,在由边长都为1的小正方形组成的网格中,点B,M均为格点,点A为小正方形边的中点.

(I)线段![]() 的长为____________;
的长为____________;
(Ⅱ)在线段![]() 上存在一点N,使得点N满足
上存在一点N,使得点N满足![]() ,请你借助给定的网格,用无刻度的直尺作出
,请你借助给定的网格,用无刻度的直尺作出![]() ,并简要说明你是怎么找到点N的.(不要求证明)_________________________________________.
,并简要说明你是怎么找到点N的.(不要求证明)_________________________________________.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直x=1线,下列结论中:①abc>0;②若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;③若方程a(x+2)(4﹣x)=﹣2的两根为x1,x2,且x1<x2,则﹣2<x1<x2<4;④(a+c)2>b2;一定正确的是______(填序号即可).
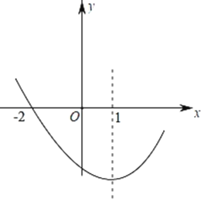
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
(1)如图1,在△ABC和△CDE中,AB=AC,EC=ED,∠BAC=∠CED,请在图中作出与△BCD相似的三角形.
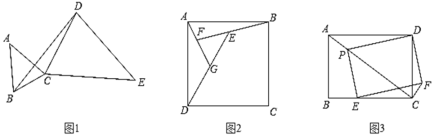
迁移应用:
(2)如图2,E为正方形ABCD内一点,∠DEB=135°,在DE上取一点G,使得BE=EG,延长BE交AG于点F,求AF:FG的值.
联系拓展:
(3)矩形ABCD中,AB=6,AD=8,P、E分别是AC、BC上的点,且四边形PEFD为矩形,若△PCD是等腰三角形时,直接写出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织1200名师生参加社会实践活动,其中包括25名教师与某公交公司洽谈后得知该公司有A、B型两种客车.每辆A型客车载客54人,租金480元;每辆B型客车载客36人,租金280元.由于每辆车上要求有一名教师,决定租用25辆客车.
设租用A型客车x辆(x为非负整数).
(Ⅰ)根据题意填写下表:
客车类型 | 车辆数(辆) | 载客数(人) | 租金(元) |
A型客车 | x | ||
B型客车 |
|
(Ⅱ)若租车总费用为10800元,怎样安排车辆?
(Ⅲ)采取怎样的租车方案可以使租车总费用最低,最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余活动情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中--项),并据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中--项),并据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
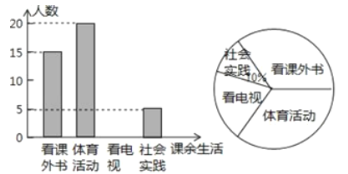
(1)![]() ,直接补全条形统计图;
,直接补全条形统计图;
(2)若该校共有学生![]() 名,试估计该校喜爱看课外书的学生人数;
名,试估计该校喜爱看课外书的学生人数;
(3)若被调查喜爱体育活动的![]() 名学生中有
名学生中有![]() 名男生和
名男生和![]() 名女生,现从这
名女生,现从这![]() 名学生中任意抽取
名学生中任意抽取![]() 名,请用列表或画树状图的方法求恰好抽到
名,请用列表或画树状图的方法求恰好抽到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好新型肺炎疫情防控,某社区开展新型肺炎疫情排查与宣传教育志愿服务活动,组织社区20名志愿者随机平均分配在4个院落门甲、乙、丙、丁处值守,并对进出人员进行测温度、劝导佩戴口罩、正确投放生活垃圾等服务.
(1)志愿者小明被分配到甲处服务是( )事件;
A.不可能事件 B.可能事件 C.必然事件 D.无法确定
(2)请用列表或树状图的方法,求出志愿者小明和小红被随机分配到同一处服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,抛物线
,抛物线![]() 图象经过
图象经过![]() 三点.
三点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上的一个动点,作
下方的抛物线上的一个动点,作![]() 于点
于点![]() ,当
,当![]() 的值最大时,求此时点
的值最大时,求此时点![]() 的坐标及
的坐标及![]() 的最大值.
的最大值.
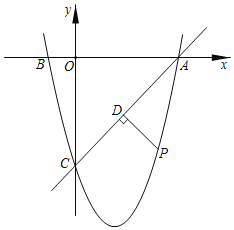
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,在平面直角坐标系xOy中,直线![]() 与y轴交于点C,与x轴交于点B,抛物线
与y轴交于点C,与x轴交于点B,抛物线![]() 经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC="2" :7.
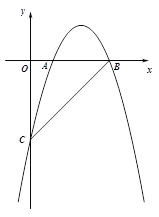


(1)求抛物线的解析式;
(2)点D为线段CB上,点P在对称轴的右侧抛物线上,PD=PB,当tan∠PDB=2,求P点的坐标;
(3)在(2)的条件下,点Q(7,m)在第四象限内,点R在对称轴的右侧抛物线上,若以点P、D、Q、R为顶点的四边形为平行四边形,求点Q、R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com