
����Ŀ�����ⱳ����
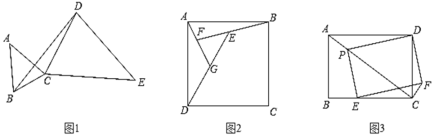
��1����ͼ1���ڡ�ABC�͡�CDE�У�AB��AC��EC��ED����BAC����CED������ͼ���������BCD���Ƶ������Σ�
Ǩ��Ӧ�ã�
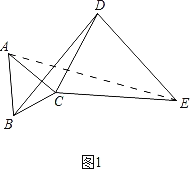
��2����ͼ2��EΪ������ABCD��һ�㣬��DEB��135������DE��ȡһ��G��ʹ��BE��EG���ӳ�BE��AG�ڵ�F����AF��FG��ֵ��
��ϵ��չ��
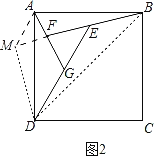
��3������ABCD�У�AB��6��AD��8��P��E�ֱ���AC��BC�ϵĵ㣬���ı���PEFDΪ���Σ�����PCD�ǵ���������ʱ��ֱ��д��CF�ij���
���𰸡���1������������2��![]() ����3��CF��3��
����3��CF��3��![]() ��
��![]() ��
��
��������
(1)��ͼ1�У�����AE�����ACE�ס�BCD����֤����BAC�ס�DEC���Ƴ�![]() ��������⣻
��������⣻
(2)��ͼ2�У���D��DM��BF��BF�ӳ�����M����AM��BD����취֤����AMF����EGF���ɵ�![]() ��
��
(3)��DJ��AC��J��֤����ADP�ס�CDF���Ƴ�![]() =
=![]() ���ɵ�CF=
���ɵ�CF=![]() =
=![]() =
=![]() PA�����������ηֱ����PA���ɽ�����⣮
PA�����������ηֱ����PA���ɽ�����⣮
(1)��ͼ1�У�����AE�����ACE�ס�BCD��
���ɣ����ڡ�ABC�͡�CDE�У�AB=AC��EC=ED����BAC=��CED��
��![]() =
=![]() ��
��
���BAC�ס�DEC��
��![]() ��
��
��AB=AC��EC=ED����BAC=��CED��
���ACB=��ABC=��DCE=��EDC��
���ACE=��BCD��
���ACE�ס�BCD��
(2)��ͼ2�У���D��DM��BF��BF�ӳ�����M����AM��BD��
�ߡ�BED=135����
���MED=45��
���MEDΪ����ֱ�������Σ�
��������ABCD��֪��ADBΪ����ֱ�������Σ�
��![]() ����
����![]() ��
��
�֡�MDE=��ADB=45����
���MDA=��EDB��
���AMD����BED��
���AMD=��BED=135������![]() ��
��
���AMF=��FEG=45����
��AM��ED��
���AMF����EGF��
![]() ��
��
(3)��ͼ3�У���DJ��AC��J��
���ı���ABCD�Ǿ��Σ�
���ADC=��BCD=90����AD=BC=8��AB=CD=6��
��AC=![]() =
=![]() =10��
=10��
��S��ADC=![]() ADDC=
ADDC=![]() ACDJ��
ACDJ��
��DJ=![]() =
=![]() ��
��
���ı���DPEF�Ǿ��Σ�
���ECD=��EFD=90����
��E��C��F��D�ĵ㹲Բ��
��E��F��D��P�ĵ㹲Բ��
��E��C��F��D��P��㹲Բ��
���PCF=��PEF=90����
���BCD=��PCF=90����
���ACB=��DCF��
��AD��BC��
���DAC=��ACB��
���DAP=��DCF��
�ߡ�ADC=��PDF=90����
���ADP=��CDF��
���ADP�ס�CDF��
��![]() =
=![]() ��
��
��CF=![]() =
=![]() =
=![]() PA��
PA��
�ٵ�DP=DCʱ��
��DJ��PC��
��CJ=PJ=![]() =
= =
=![]() ��
��
��PA=10��![]() =
=![]() ��
��
��CF=![]() ��
��![]() =
=![]() ��
��
�ڵ�CD=CP=6ʱ��PA=10��6=4��CF=![]() ��4=3��
��4=3��
�۵�PD=PCʱ��PA=PC=PD=5��
��CF=![]() ��5=
��5=![]() ��
��
����������CF=3��![]() ��
��![]()


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=30������ACB=90����BC=2��D��AB�ϵĶ��㣬���߶�CD�Ƶ�C��ʱ����ת90�����õ��߶�CE������BE����BE����Сֵ�ǣ� ��
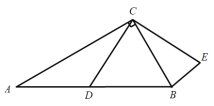
A.![]() -1B.
-1B.![]() C.
C.![]() D.2
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������ֱ��������![]() ��
��![]() ��
��![]() ��
��![]() �IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯��ϴ�ȣ�
�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯��ϴ�ȣ�
��1���������һ�ſ�Ƭ�������������ִ���![]() �ĸ���Ϊ ��
�ĸ���Ϊ ��
��2���������һ�ſ�Ƭ�������µ����ſ�Ƭ���ٷ���һ�ţ��������ſ�Ƭ������������֮����ż���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA�ǡ�O�����ߣ�A���е㣬AC��ֱ����AB���ң�����PB��PC��PC��AB�ڵ�E����PA=PB��
��1����֤��PB�ǡ�O�����ߣ�
��2������APC=3��BPC����![]() ��ֵ��
��ֵ��
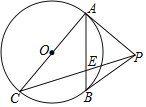
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼMΪ�߶�AB���е㣬AE��BD���ڵ�C����DME����A����B��45������DM��AC��F��ME��BC��G������FG����AB��![]() ��AF��3����BG��_____��FG��_____��
��AF��3����BG��_____��FG��_____��
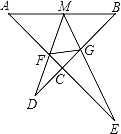
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������
������![]() ����
����![]() ����x�ύ����һ��C������ΪD������
����x�ύ����һ��C������ΪD������![]() ��
��
��������������ߵĽ���ʽ��
��������PΪ����������һ���㣨���B��C���غϣ������P�ĺ�����Ϊt��
�ٵ���P��ֱ��![]() ���·��˶�ʱ����
���·��˶�ʱ����![]() ��������ֵ��
��������ֵ��
�ڸ����������Ƿ���ڵ�P��ʹ��![]() �������ڣ���ֱ��д����P�������������ڣ���˵�����ɣ�
�������ڣ���ֱ��д����P�������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ɱ߳���Ϊ1��С��������ɵ������У���B��M��Ϊ��㣬��AΪС�����αߵ��е㣮

��I���߶�![]() �ij�Ϊ____________��
�ij�Ϊ____________��
�������߶�![]() �ϴ���һ��N��ʹ�õ�N����
�ϴ���һ��N��ʹ�õ�N����![]() ����������������������̶ȵ�ֱ������
����������������������̶ȵ�ֱ������![]() ������Ҫ˵��������ô�ҵ���N�ģ�����Ҫ��֤����_________________________________________��
������Ҫ˵��������ô�ҵ���N�ģ�����Ҫ��֤����_________________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�
�У�![]() Ϊ�Խ��ߣ���
Ϊ�Խ��ߣ���![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() .
.

��1����![]() ����֤���ı���
����֤���ı���![]() ��������
��������
��2����֪![]() ����
����![]() �ij���
�ij���
��3����![]() �̶�����
�̶�����![]() ����
����![]() ���ŵ�
���ŵ�![]() �ӵ�
�ӵ�![]() ��ʼ��ʱ����ת�����У�����
��ʼ��ʱ����ת�����У�����![]() Ҳ��֮�仯����
Ҳ��֮�仯����![]() ����
����![]() ����
����![]() ��ֱ�������Σ�ֱ��д��
��ֱ�������Σ�ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�ڣ�A��BΪx�������㣬��ABΪֱ���ġ�M��y����C��D���㣬CΪ![]() ���е㣬��AE��y���ڵ�F���ҵ�A������Ϊ(��2��0)��CD��8��
���е㣬��AE��y���ڵ�F���ҵ�A������Ϊ(��2��0)��CD��8��
��1�����M�İ뾶��
��2������P�ڡ�M��Բ�����˶�������ͼ1����EPƽ�֡�AEBʱ����PN��EP��ֵ������ͼ2������D����M�����߽�x���ڵ�Q������P���A��B���غ�ʱ��![]() �Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ���˵�����ɣ�
�Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ���˵�����ɣ�

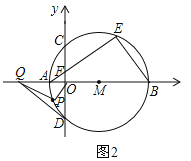
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com