
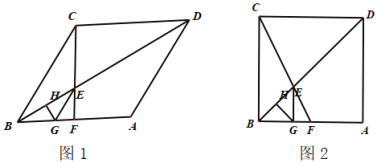
【题目】已知菱形![]() 中,
中,![]() 为对角线,点
为对角线,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)若![]() ,求证:四边形
,求证:四边形![]() 是正方形
是正方形
(2)已知![]() ,求
,求![]() 的长;
的长;
(3)若![]() 固定,设
固定,设![]() ,将
,将![]() 绕着点
绕着点![]() 从点
从点![]() 开始逆时针旋转过程中,菱形
开始逆时针旋转过程中,菱形![]() 也随之变化,且
也随之变化,且![]() 满足
满足![]() ,若
,若![]() 是直角三角形,直接写出
是直角三角形,直接写出![]() 的值;
的值;
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由菱形的性质可得![]() ,由垂直平分线的性质可得,
,由垂直平分线的性质可得,![]() ,由等边对等角可得:
,由等边对等角可得:![]() ,等量代换可得
,等量代换可得![]() ,由平行线的判定及性质可得
,由平行线的判定及性质可得![]() ,
,![]() =90°,继而由正方形的判定求证结论;
=90°,继而由正方形的判定求证结论;
(2)由菱形的性质可知,![]() ,由相似三角形的判定可得
,由相似三角形的判定可得![]() ,继而由相似三角形对应边成比例的性质可得:
,继而由相似三角形对应边成比例的性质可得:![]() ,根据题(1)可知
,根据题(1)可知![]() ,进而可证△BGE∽△BAD,由此可知
,进而可证△BGE∽△BAD,由此可知![]() ,代入数据,求出
,代入数据,求出![]() ,最后由线段垂直平分线的性质求解;
,最后由线段垂直平分线的性质求解;
(3)根据题意,从旋转过程中可看出,线段![]() 在旋转360°的过程中,
在旋转360°的过程中,![]() 由0°增大到90°再减小到0°再增加到90°再到0°,据此结合图形即可求解.
由0°增大到90°再减小到0°再增加到90°再到0°,据此结合图形即可求解.
解:(1)∵四边形![]() 是菱形
是菱形
∴![]() ,∴
,∴![]() ,∵
,∵![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]()
∴![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ∴
∴![]() ∵
∵![]() ,
,
∴![]() ∵四边形
∵四边形![]() 是菱形
是菱形
∴四边形![]() 是正方形
是正方形
(2)∵四边形![]() 是菱形
是菱形
∴![]() ,∴
,∴![]() ;
;
∴![]() ∴
∴![]()
∵![]() ∴△BGE∽△BAD,∴
∴△BGE∽△BAD,∴![]()
∵![]() ∴
∴![]()
∵![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ∴
∴![]() .
.
(3)若![]() 是直角三角形时
是直角三角形时![]() 的值可能是60°,90°,270°或300°
的值可能是60°,90°,270°或300°
∵从旋转过程中可看出,线段![]() 在旋转360°的过程中,
在旋转360°的过程中,![]() 由0°增大到90°再减小到0°再增加到90°再到0°
由0°增大到90°再减小到0°再增加到90°再到0°
∴第一次出现![]() 是直角三角形时,如图1所示,此时
是直角三角形时,如图1所示,此时![]() 为
为![]() 的一半,可得旋转角度
的一半,可得旋转角度![]() 即
即![]() 为60°;第二次出现
为60°;第二次出现![]() 是直角三角形时,如图2所示,此时(1)中已证明旋转角度
是直角三角形时,如图2所示,此时(1)中已证明旋转角度![]() 即
即![]() 为90°;当继续旋转时
为90°;当继续旋转时![]() 到达
到达![]() 的下方,同理可得旋转角度
的下方,同理可得旋转角度![]() 为270°和300°.
为270°和300°.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】已知圆锥的高为![]() ,母线为
,母线为![]() ,且
,且![]() ,圆锥的侧面展开图为如图所示的扇形.将扇形沿
,圆锥的侧面展开图为如图所示的扇形.将扇形沿![]() 折叠,使
折叠,使![]() 点恰好落在
点恰好落在![]() 上的
上的![]() 点,则弧长
点,则弧长![]() 与圆锥的底面周长的比值为( )
与圆锥的底面周长的比值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
(1)如图1,在△ABC和△CDE中,AB=AC,EC=ED,∠BAC=∠CED,请在图中作出与△BCD相似的三角形.
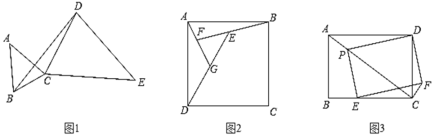
迁移应用:
(2)如图2,E为正方形ABCD内一点,∠DEB=135°,在DE上取一点G,使得BE=EG,延长BE交AG于点F,求AF:FG的值.
联系拓展:
(3)矩形ABCD中,AB=6,AD=8,P、E分别是AC、BC上的点,且四边形PEFD为矩形,若△PCD是等腰三角形时,直接写出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余活动情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中--项),并据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中--项),并据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
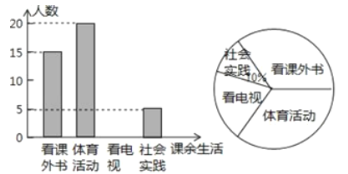
(1)![]() ,直接补全条形统计图;
,直接补全条形统计图;
(2)若该校共有学生![]() 名,试估计该校喜爱看课外书的学生人数;
名,试估计该校喜爱看课外书的学生人数;
(3)若被调查喜爱体育活动的![]() 名学生中有
名学生中有![]() 名男生和
名男生和![]() 名女生,现从这
名女生,现从这![]() 名学生中任意抽取
名学生中任意抽取![]() 名,请用列表或画树状图的方法求恰好抽到
名,请用列表或画树状图的方法求恰好抽到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好新型肺炎疫情防控,某社区开展新型肺炎疫情排查与宣传教育志愿服务活动,组织社区20名志愿者随机平均分配在4个院落门甲、乙、丙、丁处值守,并对进出人员进行测温度、劝导佩戴口罩、正确投放生活垃圾等服务.
(1)志愿者小明被分配到甲处服务是( )事件;
A.不可能事件 B.可能事件 C.必然事件 D.无法确定
(2)请用列表或树状图的方法,求出志愿者小明和小红被随机分配到同一处服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A,B,D,E为格点,C为![]() ,
,![]() 的延长线的交点.
的延长线的交点.
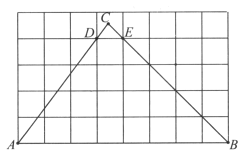
(Ⅰ)![]() 的结果为_________________.
的结果为_________________.
(Ⅱ)若点R在线段![]() 上,点S在线段
上,点S在线段![]() 上,点T在线段
上,点T在线段![]() 上,且满足四边形
上,且满足四边形![]() 为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形
为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形![]() ,并简要说明点R,S,T的位置是如何找到的(不要求证明)____________________.
,并简要说明点R,S,T的位置是如何找到的(不要求证明)____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
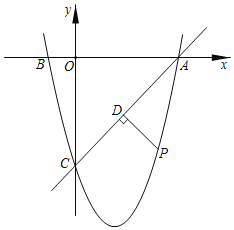
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,抛物线
,抛物线![]() 图象经过
图象经过![]() 三点.
三点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上的一个动点,作
下方的抛物线上的一个动点,作![]() 于点
于点![]() ,当
,当![]() 的值最大时,求此时点
的值最大时,求此时点![]() 的坐标及
的坐标及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有六张正面分别标有数字﹣2,﹣1,0,1,2,3的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,将该卡片上的数字加1记为b,则函数y=ax2+bx+2的图象过点(1,3)的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
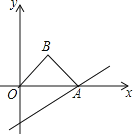
【题目】如图,直线y=![]() x﹣2与x轴交于点A,以OA为斜边在x轴的上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=
x﹣2与x轴交于点A,以OA为斜边在x轴的上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=![]() x﹣2上时,则线段AB在平移过程中扫过部分的图形面积为_____.
x﹣2上时,则线段AB在平移过程中扫过部分的图形面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com