练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在每个小正方形的边长为1的网格中，A，B，D，E为格点，C为，的延长线的交点.

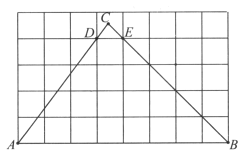
    （Ⅰ）的结果为_________________.

    （Ⅱ）若点R在线段上，点S在线段上，点T在线段上，且满足四边形为菱形，请在如图所示的网格中，用无刻度的直尺，画出菱形，并简要说明点R，S，T的位置是如何找到的（不要求证明）____________________.

    【答案】； 见解析；

    【解析】

    （Ⅰ）根据题意利用，进行分析计算即可得出答案；

    （Ⅱ）根据题意利用菱形的性质即对角线互相垂直平分进行分析即可.

    解：（Ⅰ）由题意可知，

    故答案为：；

    （Ⅱ）如图，取格点F，G，H,连接GH，连接AF分别交GH，BC于点O，S;取AC与网格线的交点为T，连接TO并延长交AB于点R.连接RS，ST得到四边形ARST即为所求.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在“五四青年节”来临之际，某校举办了以“我的青春我做主”为主题的演讲比赛．并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计（等级记为：优秀，：良好，：一般，：较差），并制作了如下统计图表（部分信息未给出）．

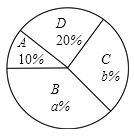
    等级

    人数

    20

    10

    请根据统计图表中的信息解答下列问题：

    （1）这次共抽取了______名参加演讲比赛的学生，统汁图中________，_______；

    （2）求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数；

    （3）若该校学生共2000人，如果都参加了演讲比赛，请你估计成绩达到优秀的学生有多少人？

    （4）若演讲比赛成绩为等级的学生中恰好有2名女生，其余的学生为男生，从等级的学生中抽取两名同学参加全市演讲比赛，请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线经过点，点，与x轴交于另一点C，顶点为D，连接．

    （１）求该抛物线的解析式；

    （２）点P为该抛物线上一动点（与点B，C不重合），设点P的横坐标为t，

    ①当点P在直线的下方运动时，求面积的最大值；

    ②该抛物线上是否存在点P，使得？若存在，请直接写出点P的坐标若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在如图所示的网格中，已知线段，现要在该网格内再确定格点和格点，某数学探究小组在探究时发现以下结论：以下结论不正确的是（ ）

    A.将线段平移得到线段，使四边形为正方形的有2种；

    B.将线段平移得到线段，使四边形为菱形的（正方形除外）有3种；

    C.将线段平移得到线段，使四边形为矩形的（正方形除外）有两种；

    D.不存在以为对角线的四边形是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知菱形中，为对角线，点是的中点，连接交于点，的垂直平分线交于点，交于点，连接.

    （1）若，求证：四边形是正方形

    （2）已知，求的长；

    （3）若固定，设，将绕着点从点开始逆时针旋转过程中，菱形也随之变化，且满足，若是直角三角形，直接写出的值；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市中心城区居民用水实行以户为单位的三级阶梯收费办法：

    第Ⅰ级：居民每户每月用水不超过18吨时，每吨收水费3元；

    第Ⅱ级：居民每户每月用水超过18吨但不超过25吨，未超过18吨的部分按照第Ⅰ级标准收费，超过的部分每吨收水费4元；

    第Ⅲ级：居民每户每月用水超过25吨，未超过25吨的部分按照第Ⅰ、Ⅱ级标准收费，超过的部分每吨收水费6元．

    现把上述水费阶梯收费办法称为方案①；假设还存在方案②：居民每户月用水一律按照每吨4元的标准缴费．

    设一户居民月用水x吨．

    （Ⅰ）根据题意填表：

    （Ⅱ）设方案①应缴水费为元，方案②应缴水费为元，分别求，关于x的函数解析式；

    （Ⅲ）当时，通过计算说明居民选择哪种付费方式更合算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店从机械厂购进甲、乙两种零件进行销售，若甲种零件每件的进价是乙种零件每件进价的，用1600元单独购进一种零件时，购进甲种零件的数量比乙种零件的数量多4件.

    （1）求每件甲种零件和每件乙种零件的进价分别为多少元?

    （2）若该商店计划购进甲、乙两种零件共110件，准备将零件批发给零售商. 甲种零件的批发价是每件100元，乙种零件的批发价是每件130元，该商店计划将这批产品全部售出从零售商处获利不低于3000元，那么该商店最多购进多少件甲种零件?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌

    粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．

    （1）试求出每天的销售量y（盒）与每盒售价 （元）之间的函数关系式；（4分）

    （2）当每盒售价定为多少元时，每天销售的利润 （元）最大？最大利润是多少？（6分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．

    （1）求证：直线DE是⊙O的切线；

    （2）若⊙O半径为1，BC＝4，求图中阴影部分的面积．

    查看答案和解析>>

    同步练习册答案