
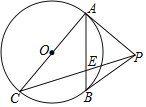
【题目】如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)若∠APC=3∠BPC,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]()
【解析】(1)如图,连接OP、OB,证明△PAO≌△PBO,根据全等三角形对应角相等可得∠PBO=∠PAO=90°,据此即可证得;
(2)连接BC,设OP交AB于K,首先证明BC=2OK,设OK=a,则BC=2a,再证明BC=PB=PA=2a,由△PAK∽△POA,可得PA2=PKPO,设PK=x,则有:x2+ax﹣4a2=0,解得x=![]() (负根已经舍弃),推出PK=
(负根已经舍弃),推出PK=![]() ,由PK∥BC,可得
,由PK∥BC,可得![]() .
.
(1)如图,连接OP、OB,
∵PA是⊙O的切线,
∴PA⊥OA,
∴∠PAO=90°,
∵PA=PB,PO=PO,OA=OB,
∴△PAO≌△PBO.
∴∠PAO=∠PBO=90°,
∴PB⊥OB,
∴PB是⊙O的切线;
(2)如图,连接BC,设OP交AB于K,
∵AB是直径,
∴∠ABC=90°,
∴AB⊥BC,
∵PA、PB都是切线,
∴PA=PB,∠APO=∠BPO,
∵OA=OB,
∴OP垂直平分线段AB,
∴OK∥BC,
∵AO=OC,
∴AK=BK,
∴BC=2OK,设OK=a,则BC=2a,
∵∠APC=3∠BPC,∠APO=∠OPB,
∴∠OPC=∠BPC=∠PCB,
∴BC=PB=PA=2a,
∵△PAK∽△POA,
∴PA2=PKPO,设PK=x,
则有:x2+ax﹣4a2=0,
解得x=![]() (负根已经舍弃),
(负根已经舍弃),
∴PK=![]() ,
,
∵PK∥BC,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=30cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=70°,则∠BEC=_____;(2)若BC=20cm,则△BCE的周长是_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成2块C型钢板和1块D型钢板;用1块B型钢板可制成1块C型钢板和3块D型钢板.现准备购买A、B型钢板共100块,并全部加工成C、D型钢板.要求C型钢板不少于120块,D型钢板不少于250块,设购买A型钢板x块(x为整数).
(1)求A、B型钢板的购买方案共有多少种?
(2)出售C型钢板每块利润为100元,D型钢板每块利润为120元.若将C、D型钢板全部出售,请你设计获利最大的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC。
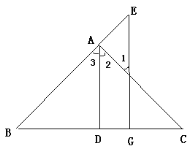
理由如下:
![]() AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知)
![]() ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( )
![]() AD‖EG,( )
AD‖EG,( )
![]() ∠1=∠2,( )
∠1=∠2,( )
=∠3,(两直线平行,同位角相等)
又![]() ∠E=∠1(已知)
∠E=∠1(已知)
![]() = (等量代换)
= (等量代换)
![]() AD平分∠BAC( )
AD平分∠BAC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
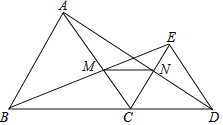
(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列表格:请你结合该表格及相关知识,求出b、c的值.即b=_________,c=___________。
列举 | 猜想 |
3、4、5 | 32=4+5 |
5、12、13 | 52=12+13 |
7、24、25 | 72=24+25 |
…… | …… |
13、b、c | 132=b+c |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.

解:∵∠1=∠B
∴AD∥( )(内错角相等,两直线平行)
∴∠C+∠2=180°,( )
∵∠C=110°.
∴∠2=( )°.
∴∠3=∠2=70°.( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com