
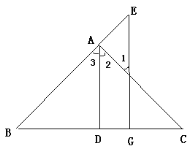
【题目】如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC。
理由如下:
![]() AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知)
![]() ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( )
![]() AD‖EG,( )
AD‖EG,( )
![]() ∠1=∠2,( )
∠1=∠2,( )
=∠3,(两直线平行,同位角相等)
又![]() ∠E=∠1(已知)
∠E=∠1(已知)
![]() = (等量代换)
= (等量代换)
![]() AD平分∠BAC( )
AD平分∠BAC( )
科目:初中数学 来源: 题型:
【题目】将正整数1至2018按一定规律排列如下表:
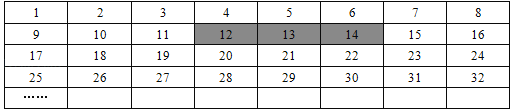
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2019 B. 2018 C. 2016 D. 2013
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的端点坐标为A(﹣1,2),B(3,1),若直线y=kx﹣2与线段AB有交点,则k的值可能是( )
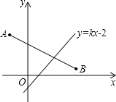
A. ﹣3B. ﹣2C. ﹣1D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
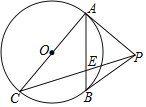
【题目】如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)若∠APC=3∠BPC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
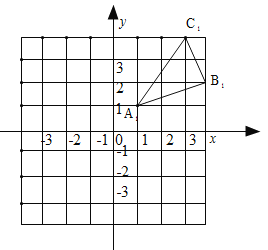
(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
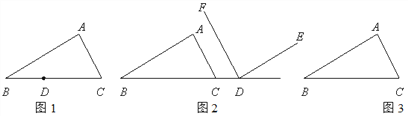
【题目】已知:△ABC和同一平面内的点D.
(1)如图1,点D在BC边上,过D作DE∥BA交AC于E,DF∥CA交AB于F.
① 依题意,在图1中补全图形;
② 判断∠EDF与∠A的数量关系,并直接写出结论(不需证明).
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A.判断DE与BA的位置关系,并证明.
(3)如图3,点D是△ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
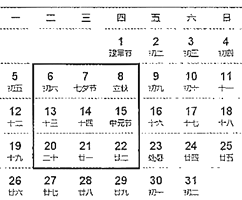
【题目】如图是某月的月历表,在此月历表上可以用一个矩形圈出![]() 个位置相邻的数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为_____.
个位置相邻的数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
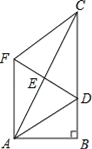
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com