
【题目】如图,在平面直角坐标系中,线段AB的端点坐标为A(﹣1,2),B(3,1),若直线y=kx﹣2与线段AB有交点,则k的值可能是( )
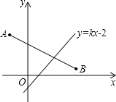
A. ﹣3B. ﹣2C. ﹣1D. 2
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
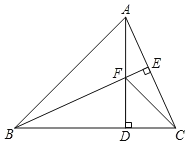
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=3![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,边AB、AC的垂直平分线分别交BC于E、F,若∠EAF=90°,AF=3,AE=4.
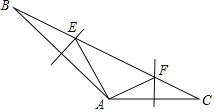
(1)求边BC的长;(2)求出∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人准备在一段长为1200m的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处,两人同时起跑.
(1)两人出发后多长时间乙追上甲?
(2)求从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数关系,并画出y(m)与时间t(s)的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC。
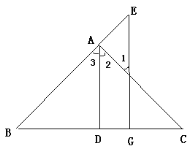
理由如下:
![]() AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知)
![]() ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( )
![]() AD‖EG,( )
AD‖EG,( )
![]() ∠1=∠2,( )
∠1=∠2,( )
=∠3,(两直线平行,同位角相等)
又![]() ∠E=∠1(已知)
∠E=∠1(已知)
![]() = (等量代换)
= (等量代换)
![]() AD平分∠BAC( )
AD平分∠BAC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A. AC,BD互相平分
B. BA=BC
C. AC=BD
D. AB∥CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com