
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯпy=ax2+bx-5гыxжсНЛгкAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌCEЁЮxжсгыХзЮяЯпЯрНЛгкЕуEЃЌЕуHЪЧжБЯпCEЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЌЙ§ЕуHЧвгыyжсЦНааЕФжБЯпгыBCЃЌCEЗжБ№НЛгкЕуFЃЌGЃЌЪдЬНОПЕБЕуHдЫЖЏЕНКЮДІЪБЃЌЫФБпаЮCHEFЕФУцЛ§зюДѓЃЌЧѓЕуHЕФзјБъМАзюДѓУцЛ§ЃЛ
ЃЈ3ЃЉШєЕуKЮЊХзЮяЯпЕФЖЅЕуЃЌЕуMЃЈ4ЃЌmЃЉЪЧИУХзЮяЯпЩЯЕФвЛЕуЃЌдкxжсЃЌyжсЩЯЪЧЗёДцдкЕуPЃЌQЃЌЪЙЫФБпаЮPQKMЕФжмГЄзюаЁЃЌШєУЛгаЃЌЫЕУїРэгЩЃЛШєгаЃЌЧѓГіЕуPЃЌQЕФзјБъЃЎ
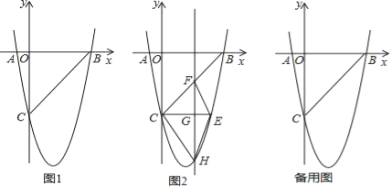
ЁОД№АИЁПЃЈ1ЃЉy=x2-4x-5ЃЛЃЈ2ЃЉHЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌУцЛ§зюДѓЮЊ
ЃЉЃЌУцЛ§зюДѓЮЊ![]() ЃЛЃЈ3ЃЉДцдкЃЌPЃЈ
ЃЛЃЈ3ЃЉДцдкЃЌPЃЈ![]() ,0ЃЉЃЌQЃЈ0ЃЌ-
,0ЃЉЃЌQЃЈ0ЃЌ-![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈжБНгЧѓГіХзЮяЯпНтЮіЪНМДПЩЃЛ
ЃЈ2ЃЉЩшHЃЈtЃЌt2Љ4tЉ5ЃЉЃЌЧѓГіжБЯпBCЕФНтЮіЪНЃЌМДПЩБэЪОГіЕуFЕФзјБъЃЌНјЖјЧѓГіЫФБпаЮCHEFЕФУцЛ§гыtЕФКЏЪ§ЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§ЧѓзюжЕМДПЩЃЛ
ЃЈ3ЃЉРћгУЖдГЦадевГіЕуPЃЌQЕФЮЛжУЃЌНјЖјЧѓГіPЃЌQЕФзјБъЃЎ
НтЃКЃЈ1ЃЉЁпЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉдкХзЮяЯпyЃНax2+bxЉ5ЩЯЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФБэДяЪНЮЊyЃНx2Љ4xЉ5ЃЌ
ЃЈ2ЃЉЩшHЃЈtЃЌt2Љ4tЉ5ЃЉЃЌ
ЁпCEЁЮxжсЃЌ
ЁрЕуEЕФзнзјБъЮЊЉ5ЃЌ
ЁпEдкХзЮяЯпЩЯЃЌ
Ёрx2Љ4xЉ5ЃНЉ5ЃЌ
ЁрxЃН0ЃЈЩсЃЉЛђxЃН4ЃЌ
ЁрEЃЈ4ЃЌЉ5ЃЉЃЌ
ЁрCEЃН4ЃЌ
ЩшжБЯпBCЕФНтЮіЪНЮЊy=kxЃЋc
НЋBЃЈ5ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ5ЃЉДњШыЃЌЕУ
![]()
НтЕУЃК![]()
ЁржБЯпBCЕФНтЮіЪНЮЊyЃНxЉ5ЃЌ
ЁрFЃЈtЃЌtЉ5ЃЉЃЌ
ЁрHFЃНtЉ5ЉЃЈt2Љ4tЉ5ЃЉЃНЉЃЈtЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁпCEЁЮxжсЃЌHFЁЮyжсЃЌ
ЁрCEЁЭHFЃЌ
ЁрSЫФБпаЮCHEFЃН![]() CEHFЃНЉ2ЃЈtЉ
CEHFЃНЉ2ЃЈtЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
Ёп-2ЃМ0
ЁрЕБt=![]() ЪБЃЌSЫФБпаЮCHEFзюДѓЃЌзюДѓжЕЮЊ
ЪБЃЌSЫФБпаЮCHEFзюДѓЃЌзюДѓжЕЮЊ![]()
ЁрHЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЫФБпаЮPQKMЕФжмГЄ=PMЃЋPQЃЋQKЃЋKMЃЈЦфжаKMЮЊЖЈжЕЃЉ
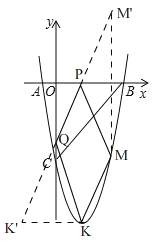
ЁпKЮЊХзЮяЯпЕФЖЅЕуЃЌy=x2-4x-5=ЃЈx-2ЃЉ2-9
ЁрKЃЈ2ЃЌЉ9ЃЉЃЌ
ЁрKЙигкyжсЕФЖдГЦЕуKЁфЃЈЉ2ЃЌЉ9ЃЉЃЌ
ЁпMЃЈ4ЃЌmЃЉдкХзЮяЯпЩЯЃЌ
Ёрm=16Ѓ16Ѓ5=-5
ЁрMЃЈ4ЃЌЉ5ЃЉЃЌ
ЁрЕуMЙигкxжсЕФЖдГЦЕуMЁфЃЈ4ЃЌ5ЃЉЃЌ
СЌНгKЁфMЁфЃЌЗжБ№НЛxжсгкЕуPЃЌНЛyжсгкЕуQ
ЁрДЫЪБPM=PMЁфЃЌQK=QKЁф
ЁрДЫЪБЫФБпаЮPQKMЕФжмГЄ=PMЃЋPQЃЋQKЃЋKM= PMЁфЃЋPQ ЃЋQKЁфЃЋKM=MЁфKЁфЃЋKMЃЌИљОнСНЕужЎМфЯпЖЮзюЖЬЃЌДЫЪБЫФБпаЮPQKMЕФжмГЄзюаЁ
ЩшжБЯпKЁфMЁфЕФНтЮіЪНЮЊyЃНexЃЋd
НЋKЁфЁЂMЁфЕФзјБъДњШыЃЌЕУ
![]()
НтЕУЃК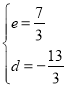
ЁржБЯпKЁфMЁфЕФНтЮіЪНЮЊyЃН![]() ЃЌ
ЃЌ
ЕБy=0ЪБЃЌНтЕУx=![]() ЃЛЕБx=0ЪБЃЌНтЕУy=
ЃЛЕБx=0ЪБЃЌНтЕУy=![]()
ЁрPЃЈ![]() ЃЌ0ЃЉЃЌQЃЈ0ЃЌЉ
ЃЌ0ЃЉЃЌQЃЈ0ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ


 гХМгОЋОэЯЕСаД№АИ
гХМгОЋОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃдкПЊеЙЖСЪщНЛСїЛюЖЏжаШЋЬхЪІЩњЛ§МЋОшЪщЃЎЮЊСЫНтЫљОшЪщМЎЕФжжРрЃЌЖдВПЗжЪщМЎНјааСЫГщбљЕїВщЃЌРюРЯЪІИљОнЕїВщЪ§ОнЛцжЦСЫШчЭМЫљЪОВЛЭъећЭГМЦЭМЃЎЧыИљОнЭГМЦЭМЛиД№ЯТУцЮЪЬтЃК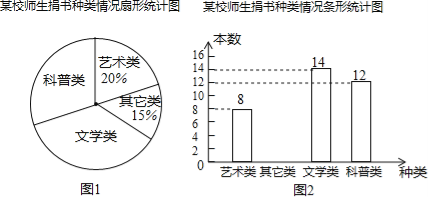
ЃЈ1ЃЉБОДЮГщбљЕїВщЕФЪщМЎгаЖрЩйБОЃПЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЧѓГіЭМ1жаБэЪОЮФбЇРрЪщМЎЕФЩШаЮдВаФНЧЖШЪ§ЃЛ
ЃЈ3ЃЉБОДЮЛюЖЏЪІЩњЙВОшЪщ1200БОЃЌЧыЙРМЦгаЖрЩйБОПЦЦеРрЪщМЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩчЧјеаФМСЫ40ЮЛОгУёВЮМгЁАжкжОГЩГЧЃЌПЙЛївпЧщЁБжОдИепЗўЮёЛюЖЏЃЌЖджОдИепвЛЬьЕФЗўЮёЪБГЄНјааЕїВщЃЌгЩЕїВщНсЙћЛцжЦСЫШчЯТВЛЭъећЕФЦЕЪ§ЗжВМБэКЭЩШаЮЭГМЦЭМЃЎ
ЦЕЪ§ЗжВМБэ
зщБ№ | ЪБМф/аЁЪБ | ЦЕЪ§/ШЫЪ§ |
Aзщ | 0Ём | 2 |
Bзщ | 1Ём | m |
Cзщ | 2Ём | 10 |
Dзщ | 3Ём | 12 |
Eзщ | 4Ём | 7 |
Fзщ |
| 4 |
ЩШаЮЭГМЦЭМ
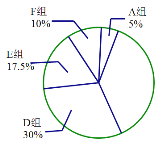
ЧыИљОнЭМБэжаЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓЦЕЪ§ЗжВМБэжаЕФ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓBзщЃЌCзщдкЩШаЮЭГМЦЭМжаЗжБ№ЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЌВЂВЙШЋЩШаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉвбжЊFзщЕФжОдИепжаЃЌжЛга1УћХЎжОдИепЃЎвЊДгИУзщжабЁШЁСНУћжОдИепЗжЗЂЩњЛюЮязЪЃЌЧыгУЪїзДЭМЛђСаБэЕФЗНЗЈЧѓ2УћжОдИЧЁКУЖМЪЧФаЪПЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+cОЙ§ЕуAЃЈЉ2ЃЌ5ЃЉЃЌгыxжсЯрНЛгкBЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ3ЃЌ0ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕуDдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЮЛгкxжсЕФЩЯЗНЃЌНЋЁїBCDбижБЯпBDЗелЕУЕНЁїBCЁфDЃЌШєЕуCЁфЧЁКУТфдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧѓЕуCЁфКЭЕуDЕФзјБъЃЛ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
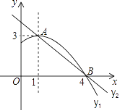
ЁОЬтФПЁПШчЭМЪЧХзЮяЯпy1=ax2+bx+cЃЈaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌХзЮяЯпЕФЖЅЕузјБъAЃЈ1ЃЌ3ЃЉЃЌгыxжсЕФвЛИіНЛЕуBЃЈ4ЃЌ0ЃЉЃЌжБЯпy2=mx+nЃЈmЁй0ЃЉгыХзЮяЯпНЛгкAЃЌBСНЕуЃЌЯТСаНсТлЃК Ђй2a+b=0ЃЛЂкabcЃО0ЃЛЂлЗНГЬax2+bx+c=3гаСНИіЯрЕШЕФЪЕЪ§ИљЃЛЂмХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЪЧЃЈЉ1ЃЌ0ЃЉЃЛЂнЕБ1ЃМxЃМ4ЪБЃЌгаy2ЃМy1 ЃЌ
Цфжае§ШЗЕФЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЁЂ
ЁЂ![]() ЪЧСНзљЯжДњЛЏГЧЪаЃЌ
ЪЧСНзљЯжДњЛЏГЧЪаЃЌ![]() ЪЧвЛИіЙХГЧвХжЗЃЌ
ЪЧвЛИіЙХГЧвХжЗЃЌ![]() ГЧдк
ГЧдк![]() ГЧЕФББЦЋЖЋ
ГЧЕФББЦЋЖЋ![]() ЃЌдк
ЃЌдк![]() ГЧЕФББЦЋЮї
ГЧЕФББЦЋЮї![]() ЃЌ
ЃЌ![]() ГЧдк
ГЧдк![]() ГЧЕФе§ЖЋЗНЯђЃЌЧв
ГЧЕФе§ЖЋЗНЯђЃЌЧв![]() ГЧгы
ГЧгы![]() ГЧЯрОр120ЧЇУзЃЌЯждк
ГЧЯрОр120ЧЇУзЃЌЯждк![]() ЁЂ
ЁЂ![]() СНГЧЪааоНЈвЛЬѕБЪжБЕФИпЫйЙЋТЗЃЎ
СНГЧЪааоНЈвЛЬѕБЪжБЕФИпЫйЙЋТЗЃЎ
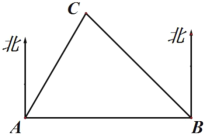
ЃЈ1ЃЉЧыФуМЦЫуЙЋТЗ![]() ЕФГЄЖШЃЈНсЙћБЃСєИљКХЃЉЃЛ
ЕФГЄЖШЃЈНсЙћБЃСєИљКХЃЉЃЛ
ЃЈ2ЃЉШєвд![]() ЮЊдВаФЃЌвд60ЧЇУзЮЊАыОЖЕФдВаЮЧјгђФкЮЊЙХМЃКЭЕиЯТЮФЮяБЃЛЄЧјЃЌЧыФуЗжЮіЙЋТЗ
ЮЊдВаФЃЌвд60ЧЇУзЮЊАыОЖЕФдВаЮЧјгђФкЮЊЙХМЃКЭЕиЯТЮФЮяБЃЛЄЧјЃЌЧыФуЗжЮіЙЋТЗ![]() ЛсВЛЛсДЉдНетИіБЃЛЄЧјЃЌВЂЫЕУїРэгЩЃЎ
ЛсВЛЛсДЉдНетИіБЃЛЄЧјЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯA=60ЁуЃЌЁЯC=75ЁуЃЌAB=8ЃЌDЁЂEЁЂFЗжБ№дкABЁЂBCЁЂCAЩЯЃЌдђЁїDEFЕФжмГЄзюаЁжЕЪЧ____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
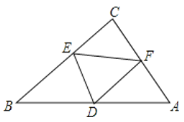
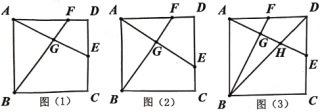
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ6ЃЌEЁЂFЗжБ№ЪЧБпCDЁЂADЩЯЖЏЕуЃЌAEКЭBFНЛгкЕуGЃЎ
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌШєEЮЊБпCDЕФжаЕуЃЌAF=2FDЃЌЧѓAGЕФГЄЃЎ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌШєЕуFдкADЩЯДгAЯђDдЫЖЏЃЌЕуEдкDCЩЯДгDЯђCдЫЖЏЃЌСНЕуЭЌЪБГіЗЂЃЌЭЌЪБЕНДяИїзджеЕуЃЌЧѓдкдЫЖЏЙ§ГЬжаЃЌЕуGдЫЖЏЕФТЗОЖГЄЃЎ
ЃЈ3ЃЉШчЭМЃЈ3ЃЉЃЌШєEЁЂFЗжБ№ЪЧБпCDЁЂADЩЯЕФжаЕуЃЌBDгыAEНЛгкЕуHЃЌЧѓЁЯFBDЕФе§ЧажЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаЯњЪлAЃЌBСНПюБЃЮТБЃЌвбжЊBПюБЃЮТБЕФЯњЪлЕЅМлБШAПюБЃЮТБЖр10дЊЃЌгУ480дЊЙКТђBПюБЃЮТБЕФЪ§СПгыгУ360дЊЙКТђAПюБЃЮТБЕФЪ§СПЯрЭЌЃЎ
ЃЈ1ЃЉA,BСНПюБЃЮТБЕФЯњЪлЕЅМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉгЩгкашЧѓСПДѓЃЌA,BСНПюБЃЮТБКмПьЪлЭъЃЌИУГЌЪаМЦЛЎдйДЮЙКНјетСНПюБЃЮТБЙВ120ИіЃЌЧвAПюБЃЮТБЕФЪ§СПВЛЩйгкBБЃЮТБЕФ2БЖЃЌAБЃЮТБЕФЪлМлВЛБфЃЌBПюБЃЮТБЕФЯњЪлЕЅМлНЕЕЭ10%ЃЌСНПюБЃЮТБЕФНјМлУПИіОљЮЊ20дЊЃЌгІШчКЮНјЛѕВХФмЪЙетХњБЃЮТБЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com