
【题目】在△ABC中,∠A=60°,∠C=75°,AB=8,D、E、F分别在AB、BC、CA上,则△DEF的周长最小值是____________.
【答案】![]()
【解析】
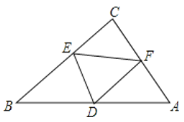
分别作点E关于AB,AC的对称点P,Q,连结AE,AP,AQ,DP,FQ,PQ,根据两点之间线段最短以及垂线段最短,即可得出△DEF周长的最小值.
解:分别作点E关于AB,AC的对称点P,Q,连结AE,AP,AQ,DP,FQ,PQ,
则DE=PD,EF=FQ,∠PAQ=2∠BAC=120°,且AP=AE=AQ,
∴∠APQ=30°,∴PQ=![]() AP.
AP.
过点A作AH⊥BC于点H,又∠B=180°-∠BAC-∠C=45°,
∴AH=ABsinB=8×sin45°=4![]() ,
,
△DEF的周长=DE+DF+EF=PD+DF+FQ≥PQ=![]() AP=
AP=![]() AE≥
AE≥![]() AH=4
AH=4![]() .
.
∴△DEF周长的最小值为4![]() .
.
故答案为:4![]() .
.


科目:初中数学 来源: 题型:
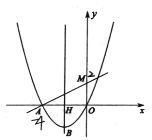
【题目】如图,已知二次函数![]() 的图像经过点
的图像经过点![]() ,顶点为
,顶点为![]() 一次函数
一次函数 ![]() 的图像交
的图像交![]() 轴于点
轴于点![]() 是抛物线上-一点,点
是抛物线上-一点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在抛物线的对称轴直线
恰好落在抛物线的对称轴直线![]() 上(对称轴直线
上(对称轴直线![]() 与
与![]() 轴交于点
轴交于点![]() ).
).
(1)求二次函数的表达式;
(2)求点![]() 的坐标;
的坐标;
(3)若点![]() 是第二象限内抛物线上一点,
是第二象限内抛物线上一点,![]() 关于抛物线的对称轴的对称点是
关于抛物线的对称轴的对称点是![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 是坐标平面内一点,若四边形
是坐标平面内一点,若四边形![]() 是正方形,求点
是正方形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
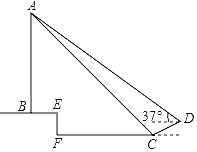
A.10.2B.9.8C.11.2D.10.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx-5与x轴交于A(-1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上是否存在点P,Q,使四边形PQKM的周长最小,若没有,说明理由;若有,求出点P,Q的坐标.
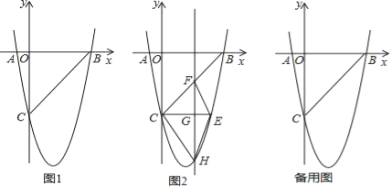
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=2 ![]() ,AD=2,点P是对角线BD上一动点(不与B,D重合),连接AP,过点P作PE⊥AP,交DC于点E,
,AD=2,点P是对角线BD上一动点(不与B,D重合),连接AP,过点P作PE⊥AP,交DC于点E,
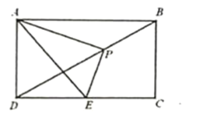
(1)求证:∠PAD=∠PEC;
(2)当点P是BD的中点时,求DE的值;
(3)在点P运动过程中,当DE= ![]() 时,求BP的值.
时,求BP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C顺时针旋转α角(0°<α<90°),得到Rt△A′B′C,A′C与AB交于点D,过点D作DE∥A′B′交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)当α=30°时,求x的值.
(2)求S与x的函数关系式,并写出x的取值范围;
(3)以点E为圆心,BE为半径作⊙E,当S=![]() 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.
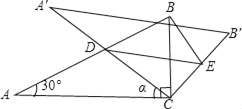
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角形纸片的两直角边AC与BC的比为3:4,首先将△ABC如图1所示折叠,使点C落在AB上,折痕为BD,然后将△ABD如图2所示折叠,使点B与点D重合,折痕为EF,则sin∠DEA的值为( )
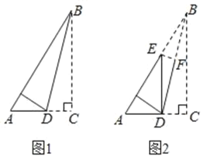
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
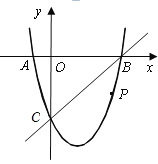
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com