
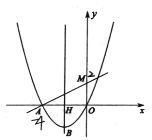
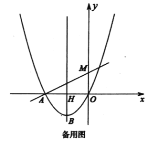
【题目】如图,已知二次函数![]() 的图像经过点
的图像经过点![]() ,顶点为
,顶点为![]() 一次函数
一次函数 ![]() 的图像交
的图像交![]() 轴于点
轴于点![]() 是抛物线上-一点,点
是抛物线上-一点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在抛物线的对称轴直线
恰好落在抛物线的对称轴直线![]() 上(对称轴直线
上(对称轴直线![]() 与
与![]() 轴交于点
轴交于点![]() ).
).
(1)求二次函数的表达式;
(2)求点![]() 的坐标;
的坐标;
(3)若点![]() 是第二象限内抛物线上一点,
是第二象限内抛物线上一点,![]() 关于抛物线的对称轴的对称点是
关于抛物线的对称轴的对称点是![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 是坐标平面内一点,若四边形
是坐标平面内一点,若四边形![]() 是正方形,求点
是正方形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点P的坐标为:(2,6)或(
;(2)点P的坐标为:(2,6)或(![]() ,
,![]() );(3)点G的坐标为:(
);(3)点G的坐标为:(![]() ,6).
,6).
【解析】
(1)直接把点A代入解析式,即可求出解析式;
(2)由题意,设点N的坐标为(![]() ,n),连接MN,过点A作AD⊥MN,AD交抛物线与点P,则点D为(
,n),连接MN,过点A作AD⊥MN,AD交抛物线与点P,则点D为(![]() ,
,![]() ),由AD⊥MN,则
),由AD⊥MN,则![]() ,求出n的值,然后求出直线AD的解析式,联合抛物线得到方程组,即可求出点P的坐标;
,求出n的值,然后求出直线AD的解析式,联合抛物线得到方程组,即可求出点P的坐标;
(3)由题意,设点G为(![]() ,
,![]() ),然后得到点E的坐标和直线OG的解析式,由点F在线段OG上,得到点F的坐标,再结合正方形的性质,有
),然后得到点E的坐标和直线OG的解析式,由点F在线段OG上,得到点F的坐标,再结合正方形的性质,有![]() ,分别求出BF、BE、EF,联立方程组,求出p的值,即可得到点G的坐标.
,分别求出BF、BE、EF,联立方程组,求出p的值,即可得到点G的坐标.
解:(1)∵二次函数![]() 的图像经过点
的图像经过点![]() ,
,
∴![]() ,
,
解得:![]() ;
;
∴二次函数的解析式为:![]() .
.
(2)由(1)知,![]() ,
,
∴顶点B为(![]() ,
,![]() ),
),
∴对称轴为![]() ;
;
在一次函数![]() 中,
中,
令![]() ,则
,则![]() ,
,
∴点M的坐标为(0,2),
设点N的坐标为(![]() ,n),
,n),
连接MN,过点A作AD⊥MN,AD交抛物线与点P,如图:
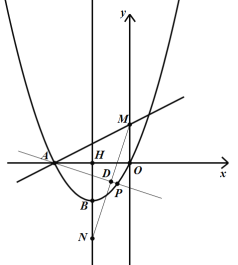
∵点M、N关于直线AP对称,
则AD垂直平分MN,即点D是MN的中点,
∴点D的坐标为(![]() ,
,![]() ),
),
∵![]() ,
,
∴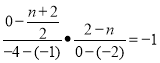 ,
,
∴![]() ,
,
解得:![]() ,
,
∴点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
结合点A(![]() ,0),可求得:
,0),可求得:
直线AD的解析式为:![]() 或
或![]() ;
;
∵抛物线的解析式为![]() ,
,
联合直线AD和抛物线,得
∴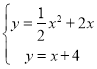 或
或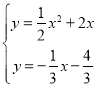 ,
,
解得: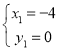 ,
,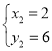 或
或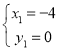 ,
,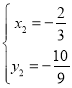 ;
;
∵点A的坐标为(![]() ,0),
,0),
∴点P的坐标为:(2,6)或(![]() ,
,![]() );
);
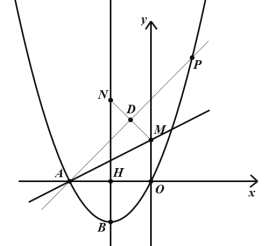
(3)由题意可知,点G在第二象限,且点G在抛物线上,四边形BDEF是正方形,连接BE、DF,如图:
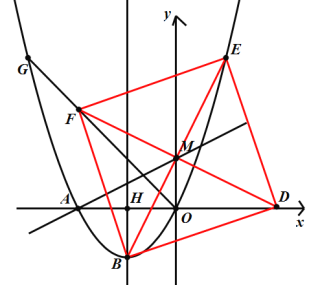
设点G为(p,![]() ),
),
∵点G与点E关于![]() 对称,
对称,
∴点E为(![]() ,
,![]() );
);
设直线OG为![]() ,则
,则
![]() ,则
,则![]() ,
,
∴直线OG为![]() ;
;
∵点F在线段OG上,则
设点F为(![]() ,
,![]() ),点F在第二象限,
),点F在第二象限,
∵四边形BDEF是正方形,
∴![]() ,
,
∵点B为(![]() ,
,![]() ),
),
∴![]() ,
,
![]() ,
,
![]() ,
,
联合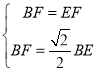 ,
,
可解得:![]() 或
或![]() ,
,
∵点F在第二象限,则![]() ,
,
∴![]() ;
;
∴![]()
∴点G的坐标为:(![]() ,6).
,6).


科目:初中数学 来源: 题型:
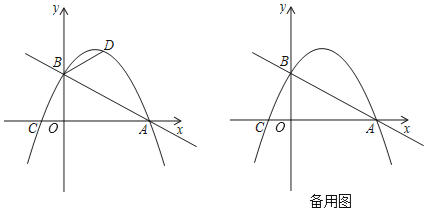
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点
与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与x轴的负半轴交于点
两点且与x轴的负半轴交于点![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 已知
已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当
和抛物线上的动点,当![]() 为顶点的四边形是平行四边形时,直接写出所有符合条件的
为顶点的四边形是平行四边形时,直接写出所有符合条件的![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
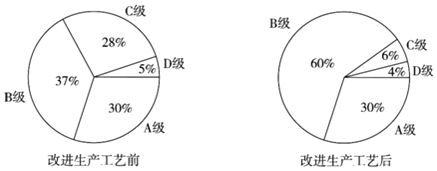
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在开展读书交流活动中全体师生积极捐书.为了解所捐书籍的种类,对部分书籍进行了抽样调查,李老师根据调查数据绘制了如图所示不完整统计图.请根据统计图回答下面问题: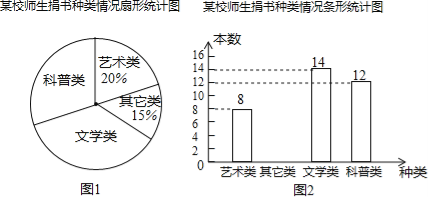
(1)本次抽样调查的书籍有多少本?请补全条形统计图;
(2)求出图1中表示文学类书籍的扇形圆心角度数;
(3)本次活动师生共捐书1200本,请估计有多少本科普类书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校初中学生在学校号召的“积极公益”活动中周末参加公益的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
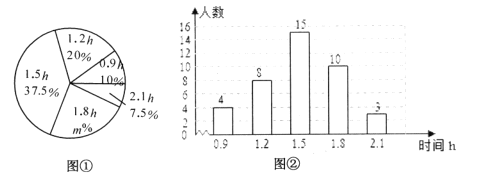
(1)本次接受调查的初中学生人数为________,图①中m的值为________;
(2)求统计的这部分学生参加公益的时间数据的平均数、众数和中位数;
(3)根据统计的这部分学生周末参加公益时间的样本数据,若该校共有650名初中学生,估计该校在这个周末参加公益时间大于1h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学开展的“好书伴我成长”读书活动中,为了解八年级320名学生读书情况,随机调查了八年级部分学生读书的册数.根据调查结果绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
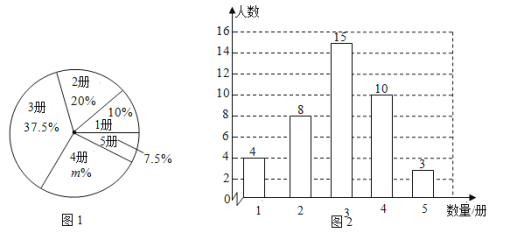
(Ⅰ)本次接受调查的学生人数为_____________,图①中m的值为______________;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)根据统计的样本数据,估计该校读书超过3册的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区招募了40位居民参加“众志成城,抗击疫情”志愿者服务活动,对志愿者一天的服务时长进行调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
频数分布表
组别 | 时间/小时 | 频数/人数 |
A组 | 0≤ | 2 |
B组 | 1≤ | m |
C组 | 2≤ | 10 |
D组 | 3≤ | 12 |
E组 | 4≤ | 7 |
F组 |
| 4 |
扇形统计图
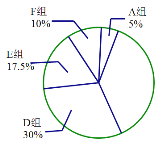
请根据图表中的信息解答下列问题:
(1)求频数分布表中的![]() 的值;
的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角的度数,并补全扇形统计图;
(3)已知F组的志愿者中,只有1名女志愿者.要从该组中选取两名志愿者分发生活物资,请用树状图或列表的方法求2名志愿恰好都是男士的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com