
【题目】在某中学开展的“好书伴我成长”读书活动中,为了解八年级320名学生读书情况,随机调查了八年级部分学生读书的册数.根据调查结果绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
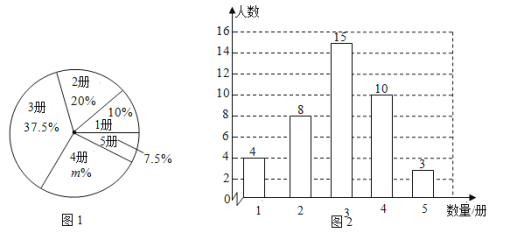
(Ⅰ)本次接受调查的学生人数为_____________,图①中m的值为______________;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)根据统计的样本数据,估计该校读书超过3册的学生人数.
【答案】(Ⅰ)40,25;(Ⅱ)平均数3,众数为3,中位数为3;(Ⅲ)104人
【解析】
(Ⅰ)本次接受调查的人数为4+8+15+10+3=40,图①中m的值为100-10-20-37.5-7.5=25;
(Ⅱ)根据平均数、众数和中位数的定义即可计算;
(Ⅲ)由扇形统计图和题(Ⅰ)可知读书超过3册的学生人数占比,再由样本估计总体的方法即可计算.
解:(Ⅰ)40,25.
(Ⅱ)平均数:![]() .
.
∵在这组样本数据中,3出现了15次,出现的次数最多,
∴这组样本数据的众数为3.
∵将这组样本数据按从小到大的顺序排列,
其中处于中间的两个数都是3,有![]() ,
,
∴这组样本数据的中位数为3.
(Ⅲ)![]() ,
,
∴根据统计的样本数据,估计该校读书超过3册的学生人数约为104人.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
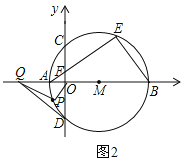
【题目】如图1,在平面直角坐标系内,A,B为x轴上两点,以AB为直径的⊙M交y轴于C,D两点,C为![]() 的中点,弦AE交y轴于点F,且点A的坐标为(﹣2,0),CD=8.
的中点,弦AE交y轴于点F,且点A的坐标为(﹣2,0),CD=8.
(1)求⊙M的半径;
(2)动点P在⊙M的圆周上运动.①如图1,当EP平分∠AEB时,求PN×EP的值;②如图2,过点D作⊙M的切线交x轴于点Q,当点P与点A,B不重合时,![]() 是否为定值?若是,请求出其值;若不是,请说明理由.
是否为定值?若是,请求出其值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
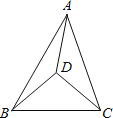
【题目】如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC=_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
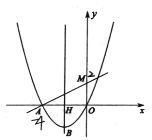
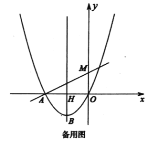
【题目】如图,已知二次函数![]() 的图像经过点
的图像经过点![]() ,顶点为
,顶点为![]() 一次函数
一次函数 ![]() 的图像交
的图像交![]() 轴于点
轴于点![]() 是抛物线上-一点,点
是抛物线上-一点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在抛物线的对称轴直线
恰好落在抛物线的对称轴直线![]() 上(对称轴直线
上(对称轴直线![]() 与
与![]() 轴交于点
轴交于点![]() ).
).
(1)求二次函数的表达式;
(2)求点![]() 的坐标;
的坐标;
(3)若点![]() 是第二象限内抛物线上一点,
是第二象限内抛物线上一点,![]() 关于抛物线的对称轴的对称点是
关于抛物线的对称轴的对称点是![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 是坐标平面内一点,若四边形
是坐标平面内一点,若四边形![]() 是正方形,求点
是正方形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
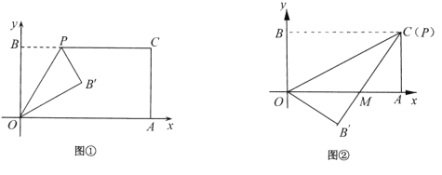
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
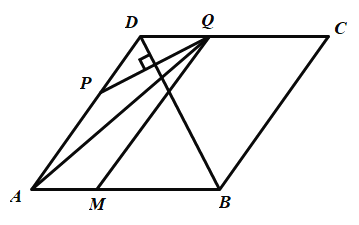
【题目】如图, 在边长为![]() 且一个内角为
且一个内角为![]() 的菱形
的菱形![]() 中, 点
中, 点![]() 以每秒
以每秒![]() 的速度从点
的速度从点![]() 出发,沿
出发,沿![]() 的路径运动,到点
的路径运动,到点![]() 停止,点
停止,点![]() 也以每秒
也以每秒![]() 的速度从点A出发,沿
的速度从点A出发,沿![]() 方向运动,到点
方向运动,到点![]() 停止,两点同时出发,过点
停止,两点同时出发,过点![]() 作
作![]() ⊥
⊥![]() ,
,![]() 与边
与边![]() (或边
(或边![]() )交于点
)交于点![]() ,
,![]() 的面积
的面积![]() 与点
与点![]() 的运动时间
的运动时间![]() (秒)的函数图象大致是( )
(秒)的函数图象大致是( )
A.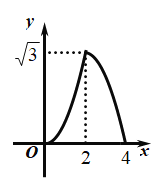 B.
B.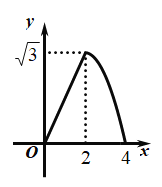
C. D.
D.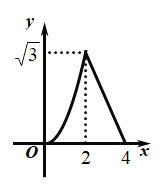
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知等边![]() , 点
, 点![]() 在射线
在射线![]() 上(不与
上(不与![]() 重合),连接
重合),连接![]() , 将射线
, 将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)如图1,当点D为线段BC中点时,请直接写出CF,BE,CD三条线段之间的数量;
(2)如图2,“点![]() 在线段
在线段![]() 上且不是
上且不是![]() 中点时,
中点时,![]() 中结论是否成立?若成立,请说明理由。若不成立,请写出正确的结论并说明理由;
中结论是否成立?若成立,请说明理由。若不成立,请写出正确的结论并说明理由;
(3)若![]() ,当
,当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
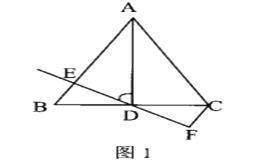
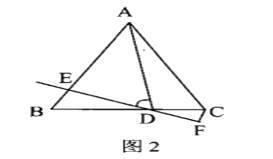
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
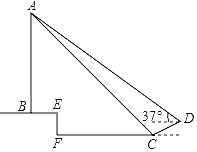
A.10.2B.9.8C.11.2D.10.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com