
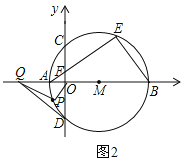
【题目】如图1,在平面直角坐标系内,A,B为x轴上两点,以AB为直径的⊙M交y轴于C,D两点,C为![]() 的中点,弦AE交y轴于点F,且点A的坐标为(﹣2,0),CD=8.
的中点,弦AE交y轴于点F,且点A的坐标为(﹣2,0),CD=8.
(1)求⊙M的半径;
(2)动点P在⊙M的圆周上运动.①如图1,当EP平分∠AEB时,求PN×EP的值;②如图2,过点D作⊙M的切线交x轴于点Q,当点P与点A,B不重合时,![]() 是否为定值?若是,请求出其值;若不是,请说明理由.
是否为定值?若是,请求出其值;若不是,请说明理由.

【答案】(1) ⊙M的半径是5;(2)①PN·PE=50; ②![]() 是定值,理由见详解.
是定值,理由见详解.
【解析】
(1)由垂径定理可知OD=4,连接MD在Rt△OMD中用勾股定理即可求出r.
(2)①连接AP、BP.当EP平分∠AEB时,可得△BAP为等腰直角三角形,求出AP=![]() ,再证△APN∽△EPA得到PN·PE= PA2,进而可得PN×EP的值;
,再证△APN∽△EPA得到PN·PE= PA2,进而可得PN×EP的值;
②![]() 是定值.由DQ与⊙M于D点,可得△QMD∽△MDO,又MD=MP,可得
是定值.由DQ与⊙M于D点,可得△QMD∽△MDO,又MD=MP,可得![]() ,进而证明△QMP∽△PMQ,即可由相似三角形性质求解.
,进而证明△QMP∽△PMQ,即可由相似三角形性质求解.
(1)如图1:
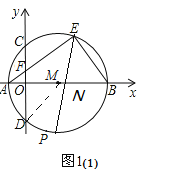
∵直径AB⊥CD,CD=8,
∴OD=![]() CD=4,
CD=4,
连接MD设MD=MA=r,
在Rt△OMD中.由OM2+OD2=MD2,
得(r﹣2)2+42=r2.解得r=5,
∴⊙M的半径是5;
(2)①如图1(2)
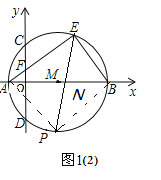
∵![]() .
.
∴![]() ,
,
∴AE=CD=8,
∵AB是直径,
∴∠AEB=90°,
连接AP,BP,
当EP平分∠AEB时,∠BAP=∠BEP=∠AEP=∠ABP=45°,
△BAP为等腰直角三角形,
∵AB=10,
∴AP=![]() ,
,
∵∠PAN=∠PEB=∠AEP, ∠APN=∠EPA,
∴△APN∽△EPA,
∴![]() ,
,
∴PN·PE= PA2=(![]() )2=50;
)2=50;
②![]() 是定值.
是定值.
理由如图2:连接PM、DM,
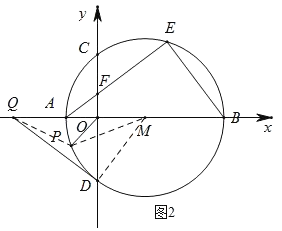
∵DQ与⊙M于D点,
∴∠MDQ=90°=∠DOM,
∴∠QMD=∠DMO,
∴△QMD∽△MDO,
∴![]() ,
,
又∵MD=MP,
∴![]() ,
,
又∵∠OMP=∠PMQ,
∴△QMP∽△PMQ,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形
(1)概念理解
①根据上述定义举一个等补四边形的例子:
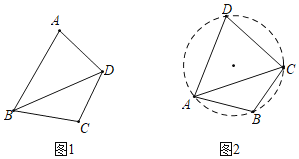
②如图1,四边形ABCD中,对角线BD平分∠ABC,∠A+∠C=180°,求证:四边形ABCD是等补四边形
(2)性质探究:
③小明在探究时发现,由于等补四边形有一组对角互补,可得等补四边形的四个顶点共圆,如图2,等补四边形ABCD内接于⊙O,AB=AD,则∠ACD ∠ACB(填“>”“<”或“=“);
④若将两条相等的邻边叫做等补四边形的“等边”,等边所夹的角叫做“等边角”,它所对的角叫做“等边补角”连接它们顶点的对角线叫做“等补对角线”,请用语言表述③中结论:
(3)问题解决
在等补四边形ABCD中,AB=BC=2,等边角∠ABC=120°,等补对角线BD与等边垂直,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
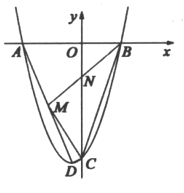
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于
与x轴交于![]() 、B两点,与y轴交点C的坐标为
、B两点,与y轴交点C的坐标为![]() ,
,![]() 为抛物线顶点,连结AD,点M为线段AD上动点(不含端点),BM与y轴交于点N.
为抛物线顶点,连结AD,点M为线段AD上动点(不含端点),BM与y轴交于点N.
(1)求抛物线解析式;
(2)是否存在点M使得![]() 与
与![]() 相似,若存在请求出点M的坐标,若不存在,请说明理由;
相似,若存在请求出点M的坐标,若不存在,请说明理由;
(3)求当BM将四边形ABCM分为面积相等的两部分时ON的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
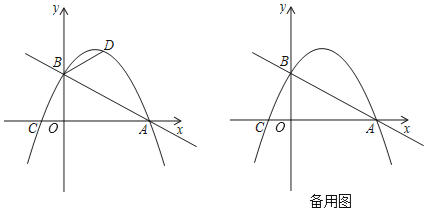
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点
与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与x轴的负半轴交于点
两点且与x轴的负半轴交于点![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 已知
已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当
和抛物线上的动点,当![]() 为顶点的四边形是平行四边形时,直接写出所有符合条件的
为顶点的四边形是平行四边形时,直接写出所有符合条件的![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,崂山区教体局对参加2018年崂山区禁毒知识竞赛的2500名初中学生的初试成绩(成绩均为整数)进行一次抽样调查,所得数据如下表:
成绩分组 | 60.5~70.5 | 70.5~80.5 | 80.5~90.5 | 90.5~100.5 |
频数 | 50 | 150 | 200 | 100 |
(1)抽取样本的总人数;
(2)根据表中数据,补全图中频数分布直方图;
(3)若规定初试成绩在90分以上(不包括90分)的学生进入决赛,则全区进入决赛的初中学生约有多少人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】延迟开学期间,学校为了全面分析学生的网课学习情况,进行了一次抽样调查(把学习情况分为三个层次,A:能主动完成老师布置的作业并合理安排课外时间自主学习;B:只完成老师布置的作业;C:不完成老师的作业),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
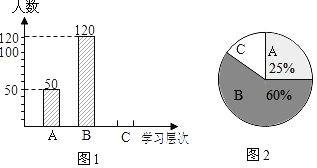
(1)此次抽样调查中,共调查了_______名学生;
(2)将条形图补充完整;
(3)求出图2中C所占的圆心角的度数;
(4)如果学校开学后对A层次的学生奖励一次看电影,根据抽样调查结果,请你估计该校1500名学生中大约有多少名学生能获得奖励?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有( )
①快车追上慢车需6小时;
②慢车比快车早出发2小时;
③快车速度为46km/h;
④慢车速度为46km/h;
⑤AB两地相距828km;
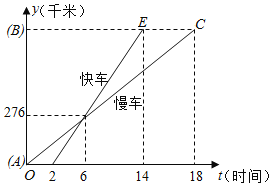
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
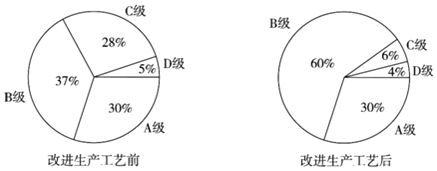
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学开展的“好书伴我成长”读书活动中,为了解八年级320名学生读书情况,随机调查了八年级部分学生读书的册数.根据调查结果绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
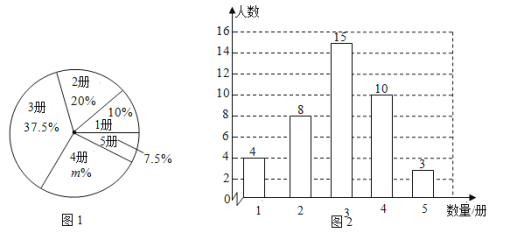
(Ⅰ)本次接受调查的学生人数为_____________,图①中m的值为______________;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)根据统计的样本数据,估计该校读书超过3册的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com