
【题目】如图1,抛物线![]() 与
与![]() 铀交于
铀交于![]() ,与
,与![]() 轴交于
轴交于![]() 抛物线的顶点为
抛物线的顶点为![]() 直线
直线![]() 过
过![]() 交
交![]() 轴于
轴于![]() .
.
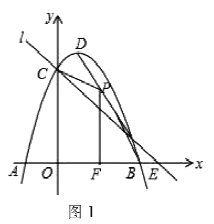
(1)写出![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(2)![]() 是线段
是线段![]() 上的动点(不与
上的动点(不与![]() 重合),
重合),![]() 轴于
轴于![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的两数关系式,并求
之间的两数关系式,并求![]() 的最大值;
的最大值;
(3)点![]() 在
在![]() 轴的正半轴上运动,过
轴的正半轴上运动,过![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于
于![]() 交抛物线于
交抛物线于![]() 连接
连接![]() ,将
,将![]() 沿
沿![]() 翻转,
翻转,![]() 的对应点为
的对应点为![]() .在图2中探究:是否存在点
.在图2中探究:是否存在点![]() ;使得
;使得![]() 恰好落在
恰好落在![]() 轴?若存在,请求出
轴?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
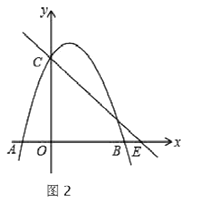
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,当
,当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ;(3)存在.点
;(3)存在.点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)先把抛物线解析式配成顶点式即可得到D点坐标,再求出C点坐标,然后利用待定系数法求直线l的解析式;
(2)先根据抛物线与x轴的交点问题求出B(3,0),再利用待定系数法求出直线BD的解析式为y=-2x+6,则P(x,-2x+6),然后根据梯形的面积公式可得![]() ,再利用二次函数的性质求S的最大值;
,再利用二次函数的性质求S的最大值;
(3)如图2,设Q(t,0)(t>0),则可表示出![]() ,利用两点间的距离公式得到
,利用两点间的距离公式得到![]() ,
,![]() ,然后证明NM=CM得到
,然后证明NM=CM得到![]() ,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
![]() ,
,
![]()
当![]() 时,
时,![]()
则![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把分别![]() 代入得
代入得![]()
解得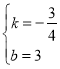 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
解得![]() ,
,
则![]()
设直线![]() 的解析式为
的解析式为![]()
把![]() 分别代入得
分别代入得![]() ,
,
解得![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]()
则![]() ,
,
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ;
;
![]() 存在.
存在.
如图2,设![]() ,
,
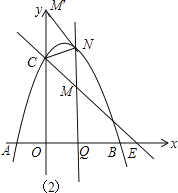
则![]()
![]()
![]() ,
,
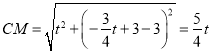 ,
,
![]() 沿
沿![]() 翻转,
翻转,![]() 的对应点为
的对应点为![]() 落在
落在![]() 轴上,
轴上,
![]() ,
,
∵![]() 轴,
轴,
![]()
![]()
![]()
![]()
![]()
当![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
此时![]() 点坐标为
点坐标为![]() ;
;
当![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
此时![]() 点坐标为
点坐标为![]() ,
,
综上所述:点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过A(-1,0)、B(4,5)三点.
的图象经过A(-1,0)、B(4,5)三点.
(1)求此二次函数的解析式;
(2)当x为何值时,y随x的增大而减小?
(3)当x为何值时,y>0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在以![]() 为原点的平面直角坐标系中,抛物线的顶点为
为原点的平面直角坐标系中,抛物线的顶点为![]() 点,且经过点
点,且经过点![]() ,
,![]() ,
,![]() 三点.
三点.
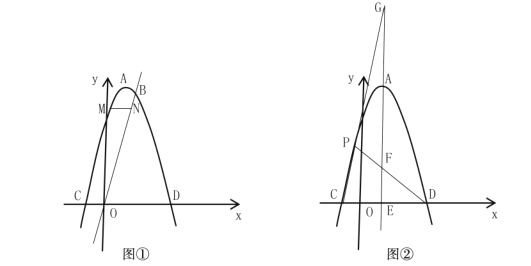
(1)求直线![]() 和该抛物线相应的函数表达式;
和该抛物线相应的函数表达式;
(2)如图①,点![]() 为抛物线上的一个动点,且在直线
为抛物线上的一个动点,且在直线![]() 的上方,过点
的上方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
(3)如图②,过点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,且
,且![]() 轴,点
轴,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,直线
之间的一个动点,直线![]() ,
,![]() 与
与![]() 分别交于
分别交于![]() ,
,![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校同安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
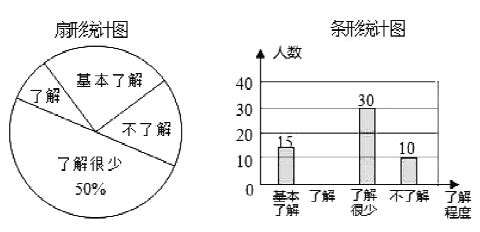
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 度;并补全条形统计图.
(2)若该中学共有学生![]() 人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的![]() 个女生
个女生![]() 和
和![]() 个男生
个男生![]() 中分别随机抽取
中分别随机抽取![]() 人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生
人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
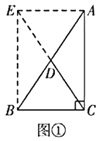
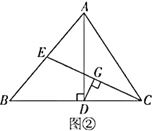
【题目】(教材呈现)下图是华师版九年级上册数学教材第103—104页的部分内容.

定理证明:请根据教材图24.2.2的提示,结合图①完成直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”的证明.
定理应用:如图②,在![]() 中,
中,![]() ,垂足为点
,垂足为点![]() (点
(点![]() 在
在![]() 上),
上),![]() 是
是![]() 边上的中线,
边上的中线,![]() 垂直平分
垂直平分![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
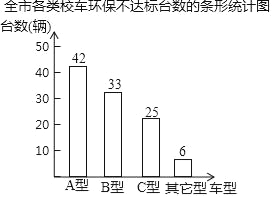
【题目】长春市对全市各类(A型、B型、C型.其它型)校车共848辆进行环保达标普查,普查结果绘制成如下条形统计图:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其它型300元/辆,求全市需要进行维修的环保不达标校车维修费的总和;
(4)若每辆校车乘坐40名学生,那么一次性维修全部不达标校车将会影响全市80000名学生乘校车上学的百分比是
查看答案和解析>>
科目:初中数学 来源: 题型:
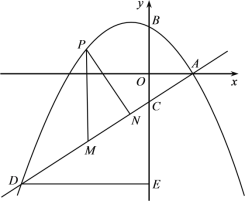
【题目】如图,抛物线![]() 与
与![]() 轴交于点A(2,0),交
轴交于点A(2,0),交![]() 轴于点B(0,
轴于点B(0,![]() ),直线
),直线![]() 过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD于点N.
过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD于点N.
⑴填空:![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
⑵探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
⑶设△PMN的周长为![]() ,点P的横坐标为x,求
,点P的横坐标为x,求![]() 与x的函数关系式,并求出
与x的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com