
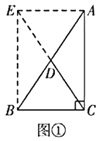
【题目】(教材呈现)下图是华师版九年级上册数学教材第103—104页的部分内容.

定理证明:请根据教材图24.2.2的提示,结合图①完成直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”的证明.
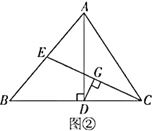
定理应用:如图②,在![]() 中,
中,![]() ,垂足为点
,垂足为点![]() (点
(点![]() 在
在![]() 上),
上),![]() 是
是![]() 边上的中线,
边上的中线,![]() 垂直平分
垂直平分![]() .求证:
.求证:![]() .
.
【答案】定理证明:见详解;定理应用:见详解.
【解析】
定理证明:延长CD到点E,使CD=DE,通过条件证明四边形EBCA为矩形,利用矩形的性质可得到结论;
定理应用:连接ED,通过定理得到DE=BE,即∠B=∠EDB,然后通过![]() 垂直平分
垂直平分![]() ,得到DE=DC,即∠DEC=∠BCE,利用三角形外角可证得结论.
,得到DE=DC,即∠DEC=∠BCE,利用三角形外角可证得结论.
定理证明:延长CD到点E,使CD=DE,连接AE、BE,
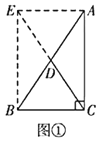
∵DC是AB边上的中线,
∴AD=BD,
又∵CD=DE,
∴四边形EBCA为平行四边形,
又∵∠ACB为直角,
∴四边形EBCA为矩形,
∴AB=CE,
∴![]() ,
,
∴直角三角形斜边上的中线等于斜边的一半;
定理应用:连接ED,
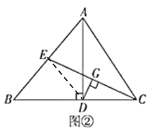
∵△ABC中,![]() 是
是![]() 边上的中线,
边上的中线,
∴E为AB的中点,
又∵![]() ,
,
∴DE是直角三角形ABD斜边上的中线,
∴DE=BE,
∴∠B=∠EDB,
∵![]() 垂直平分
垂直平分![]() ,
,
∴DE=DC,
∴∠DEC=∠BCE,
∵∠EDB=∠DEC+∠BCE,
∴∠EDB=2∠BCE,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() .
.

(1)求该抛物线和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的动点,设
上方抛物线上的动点,设![]() 点的横坐标为
点的横坐标为![]() ,试用含
,试用含![]() 的代数式表示
的代数式表示![]() 的面积,并求出
的面积,并求出![]() 面积的最大值;
面积的最大值;
(3)设P点是直线![]() 上一动点,
上一动点,![]() 为抛物线上的点,是否存在点
为抛物线上的点,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、P、
、P、![]() 为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点
为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点![]() 坐标,不存在说明理由.
坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月5日,我校组织全体学生参加了“走出校门,服务社会”的活动.九年级三班同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图.请根据同学所作的两个图形.解答:
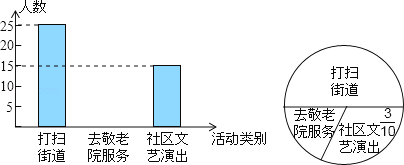
(1)九年级三班有多少名学生;
(2)补全直方图的空缺部分;
(3)若九年级有800名学生,估计该年级去敬老院的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 铀交于
铀交于![]() ,与
,与![]() 轴交于
轴交于![]() 抛物线的顶点为
抛物线的顶点为![]() 直线
直线![]() 过
过![]() 交
交![]() 轴于
轴于![]() .
.
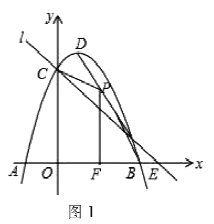
(1)写出![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(2)![]() 是线段
是线段![]() 上的动点(不与
上的动点(不与![]() 重合),
重合),![]() 轴于
轴于![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的两数关系式,并求
之间的两数关系式,并求![]() 的最大值;
的最大值;
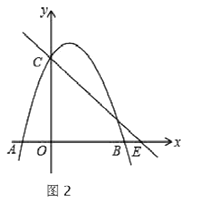
(3)点![]() 在
在![]() 轴的正半轴上运动,过
轴的正半轴上运动,过![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于
于![]() 交抛物线于
交抛物线于![]() 连接
连接![]() ,将
,将![]() 沿
沿![]() 翻转,
翻转,![]() 的对应点为
的对应点为![]() .在图2中探究:是否存在点
.在图2中探究:是否存在点![]() ;使得
;使得![]() 恰好落在
恰好落在![]() 轴?若存在,请求出
轴?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
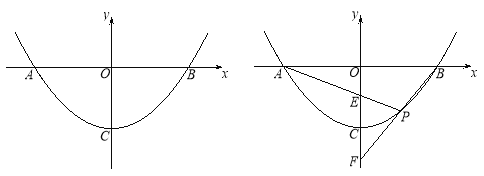
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线,![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且抛物线
,且抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
(1)抛物线的表达式;
(2)若抛物线![]() 与抛物线
与抛物线![]() 关于直线
关于直线![]() 对称,抛物线
对称,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),要使
左侧),要使![]() ,求所有满足条件的抛物线
,求所有满足条件的抛物线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长为2cm,∠A=60°,点M从点A出发,以1cm/s的速度向点B运动,点N从点A同时出发,以2cm/s的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动.则△AMN的面积y(cm2)与点M运动的时间t(s)的函数的图象大致是( )
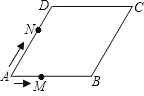
A. 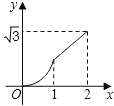 B.
B. 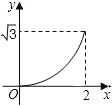
C. 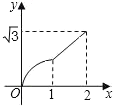 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com