
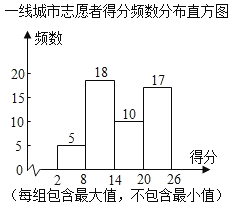
【题目】为了解疫情对精神负荷造成的影响,某机构分别在一线城市和三线城市的志愿者中随机选取了50人参加LES测试,根据志愿者的答题情况计算出LES得分,并对得分进行整理,描述和分析,部分信息如下:
一、三线城市志愿者得分统计表
城市 | 中位数 | 平均数 |
一线城市 | a | 17.6 |
三线城市 | 14 | 17.2 |
注:一线城市在14<x≤20中的得分是:15,15,16,17,17,17,17,18,18,20.
根据以上信息,解答下列问题:
(1)表中a的值为 ;
(2)得分越低反映个体承受的精神压力越小,排名越靠前,在这次调查中,一线城市的志愿者甲和三线城市的志愿者乙的得分均为15分,请判断甲、乙在各自城市选取的志愿者中得分排名谁更靠前,并说明理由;
(3)如果得分超过平均数就需要进行心理干预,请估计一线城市全部2000名志愿者中有多少人需要进行心理干预?
【答案】(1)15.5;(3)三线城市的志愿者乙在各自城市选取的志愿者中得分排名更靠前,理由见解析;(4)800人.
【解析】
(1)先根据图表确定一线城市2≤x<14的有23人,所以第25、26个数在14<x≤20这一组,根据已知求解即可;
(2)根据一线城市和三线城市的中位数,与15进行比较,可以得出结论;
(3)通过统计图表得出一线城市需要心理干预的人数,求出百分比,用总人数乘以百分比即可求解.
(1)∵2≤x<14的有5+18=23(人),一线城市在14<x≤20这一组的是:15,15,16,17,17,17,17,18,18,20,在一线城市和三线城市的志愿者中随机选取了50人参加LES测试,∴a=(15+16)÷2=15.5.
故答案为:15.5;
(3)在这次测试中,一线城市的志愿者甲和三线城市的志愿者乙的得分均为15分,三线城市的志愿者乙在各自城市选取的志愿者中得分排名更靠前,
理由:∵一线城市的志愿者甲的中位数是15.5,三线城市的志愿者乙的中位数是14,
∴在这次测试中,三线城市的志愿者乙在各自城市选取的志愿者中得分排名更靠前;
(4)2000![]() 800(人),
800(人),
答:估计一线城市全部2000名志愿者中有800人需要进行心理干预.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
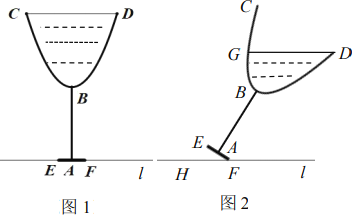
【题目】图1是一个高脚杯截面图,杯体![]() 呈抛物线状(杯体厚度不计),点
呈抛物线状(杯体厚度不计),点![]() 是抛物线的顶点,
是抛物线的顶点,![]() ,点
,点![]() 是
是![]() 的中点,当高脚杯中装满液体时,液面
的中点,当高脚杯中装满液体时,液面![]() ,此时最大深度(液面到最低点的距离)为
,此时最大深度(液面到最低点的距离)为![]() ,将高脚杯绕点
,将高脚杯绕点![]() 缓缓倾斜倒出部分液体,当
缓缓倾斜倒出部分液体,当![]() 时停止,此时液面为
时停止,此时液面为![]() ,则液面
,则液面![]() 到平面
到平面![]() 的距离是________________;此时杯体内液体的最大深度为_____________________.
的距离是________________;此时杯体内液体的最大深度为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸板和圆形纸板按如图方式分别剪得同样大定理特例图(AC=3,BC=4,AB=5,分别以三边长向外剪正方形) ,图1中边HI、LM和点K、J都恰好在矩形纸板的边上,图2中的圆心O在AB中点处,点H、I都在圆上,则矩形和圆形纸板的面积比是( )
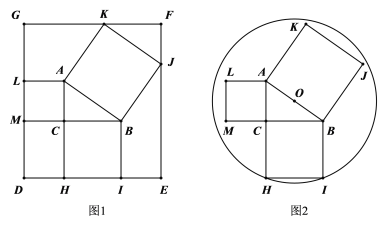
A.400:127πB.484:145πC.440:137πD.88:25π
查看答案和解析>>
科目:初中数学 来源: 题型:
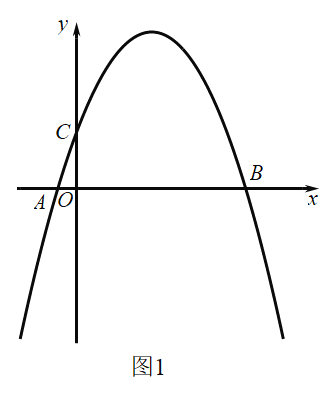
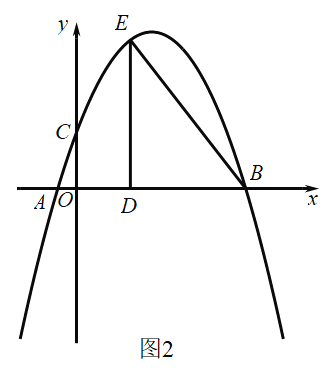
【题目】已知:在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右边)交
的右边)交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)如图1,求抛物线的解析式;
(2)如图2,点![]() 是第一象限抛物线上的点,连接
是第一象限抛物线上的点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
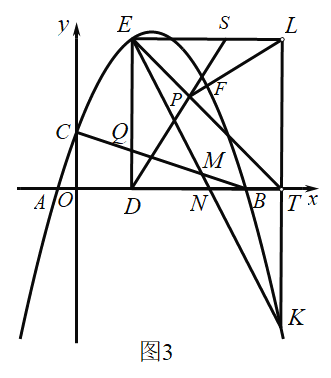
(3)如图3,在(2)的条件下,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是第四象限抛物线上的点,连接
是第四象限抛物线上的点,连接![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,点
,点![]() 是抛物线对称轴右侧第一象限抛物线上的点,连接
是抛物线对称轴右侧第一象限抛物线上的点,连接![]() 、
、![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() .求点
.求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与一直线相交于
与一直线相交于![]() ,
,![]() 两点.
两点.
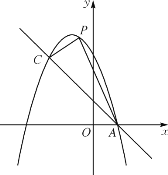
(1)求抛物线的函数表达式;
(2)求直线![]() 的函数表达式;
的函数表达式;
(3)若![]() 是抛物线上位于直线
是抛物线上位于直线![]() 上方的一个动点,求
上方的一个动点,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有 ![]() 名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个不完整的统计图.请根据相关信息,解答下列问题:
名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个不完整的统计图.请根据相关信息,解答下列问题:
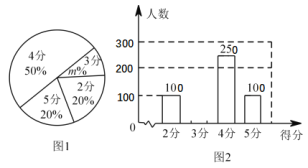
(1)本次参加跳绳测试的学生人数为 ,图 ![]() 中
中 ![]() 的值为 ;
的值为 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校九年级跳绳测试中得 ![]() 分的学生约有多少人?
分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
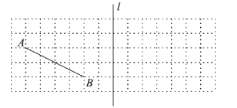
【题目】如图,在![]() 的网格中,每个小正方形的边长都为
的网格中,每个小正方形的边长都为![]() .网格线的交点称为格点,以格点为顶点的三角形称为格点三角形.已知直线
.网格线的交点称为格点,以格点为顶点的三角形称为格点三角形.已知直线![]() 及格点
及格点![]() ,
,![]() ,连接
,连接![]() .
.
(1)请根据以下要求依次画图:
①在直线![]() 的左边画出一个格点
的左边画出一个格点![]() (点
(点![]() 不在直线
不在直线![]() 上),且满足格点
上),且满足格点![]() 是直角三角形;
是直角三角形;
②画出![]() 关于直线
关于直线![]() 的轴对称
的轴对称![]() .
.
(2)满足(1)的![]() 面积的最大值为多少?
面积的最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
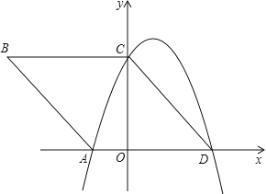
【题目】如图,在平面直角坐标系xOy中,四边形ABCD是边长为5的菱形,顶点A.C.D均在坐标轴上,sinB=![]() .
.
(1)求过A,C,D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1>y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A,E两点之间的一个动点,且直线PE交x轴于点F,问:当P点在何处时,△PAE的面积最大?并求出面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为
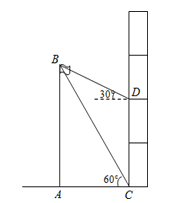
A.9米B.6![]() 米C.6米D.(6+
米C.6米D.(6+![]() )米
)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com