
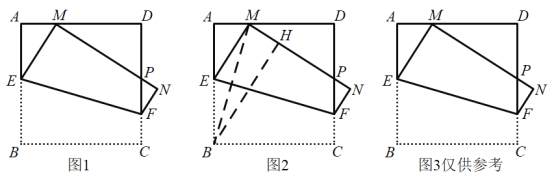
ЁОЬтФПЁПШчЭМ1ЃЌдкБпГЄЮЊ1ЕФе§ЗНаЮABCDжаЃЌЖЏЕуEЃЌFЗжБ№дкБпABЃЌCDЩЯЃЌНЋе§ЗНаЮABCDбижБЯпEFелЕўЃЌЪЙЕуBЕФЖдгІЕуMЪМжеТфдкБпADЩЯ(ЕуMВЛгыЕуAЃЌDжиКЯ)ЃЌЕуCТфдкЕуNДІЃЌMNгыCDНЛгкЕуPЃЌЩшBEЃНxЃЎ
(1)ЕБAMЃН![]() ЪБЃЌЧѓxЕФжЕЃЛ
ЪБЃЌЧѓxЕФжЕЃЛ
(2)ШчЭМ2ЃЌСЌНгBMЁЂЙ§BЕузїBHЁЭMNЃЌДЙзуЮЊHЃЌЧѓжЄЃКBMЪЧЁЯABHЕФНЧЦНЗжЯпЃЛ
(3)ЫцзХЕуMдкБпADЩЯЮЛжУЕФБфЛЏЃЌЁїPDMЕФжмГЄЪЧЗёЗЂЩњБфЛЏЃПШчБфЛЏЃЌЧыЫЕУїРэгЩЃЛШчВЛБфЃЌЧыЧѓГіИУЖЈжЕЃЛ
(4)ЩшЫФБпаЮBEFCЕФУцЛ§ЮЊSЃЌЧѓSгыxжЎМфЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіSЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉxЃН![]() ЃЎЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉВЛБфЃЌЁїDMPЕФжмГЄЮЊ2ЃЛЃЈ4ЃЉSЃН
ЃЎЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉВЛБфЃЌЁїDMPЕФжмГЄЮЊ2ЃЛЃЈ4ЃЉSЃН![]() (2xЃ
(2xЃ![]() )ЃЌУцЛ§ЕФзюаЁжЕЮЊ
)ЃЌУцЛ§ЕФзюаЁжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЙДЙЩЖЈРэЙЙНЈЗНГЬЃЌМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЭЈЙ§жЄУїЁїBAMЁеЁїBHMНјЖјПЩЕУЁЯABMЃНЁЯMBHЃЌМДПЩЕУжЄЃЛ
ЃЈ3ЃЉЩшAMЃНyЃЌдђBEЃНEMЃНxЃЌMDЃН1ЉyЃЌдкRtЁїAEMжаЃЌгЩЙДЙЩЖЈРэЕУГіxЁЂyЕФЙиЯЕЪНЃЌПЩжЄRtЁїAEMЁзRtЁїDMPЃЌИљОнЯрЫЦШ§НЧаЮЕФжмГЄБШЕШгкЯрЫЦБШЧѓЁїDMPЕФжмГЄЃЛ
ЃЈ4ЃЉзїFHЁЭABгкHЃЎдђЫФБпаЮBCFHЪЧОиаЮЃЎСЌНгBMНЛEFгкOЃЌНЛFHгкKЃЎИљОнЬнаЮЕФУцЛ§ЙЋЪНЙЙНЈЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪНтОізюжЕЮЪЬтМДПЩЃЛ
НтЃКЃЈ1ЃЉШчЭМЃЌдкRtЁїAEMжаЃЌAEЃН1ЉxЃЌEMЃНBEЃНxЃЌAMЃН![]() ЃЌ
ЃЌ
ЁпAE2+AM2ЃНEM2ЃЌ
ЁрЃЈ1ЉxЃЉ2+ЃЈ![]() ЃЉ2ЃНx2ЃЌ
ЃЉ2ЃНx2ЃЌ
ЁрxЃН![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЁпEBЃНEMЃЌ
ЁрЁЯEBMЃНЁЯEMBЃЎ
ЁпЁЯEBCЃНЁЯEMNЃЌ
ЁрЁЯMBCЃНЁЯBMNЃЎ
ЁпADЁЮBCЃЌ
ЁрЁЯMBCЃНЁЯAMBЃЌ
ЁрЁЯAMBЃНЁЯBMNЃЌ
гжЁпЁЯAЃНЁЯMHBЃЌBMЃНBMЃЌ
ЁрЁїBAMЁеЁїBHMЃЎ
ЁрЁЯABMЃНЁЯMBHЃЌ
ЁрBMЪЧЁЯABHЕФНЧЦНЗжЯпЃЛ
ЃЈ3ЃЉЁїDMPЕФжмГЄВЛБфЃЌЮЊ2ЃЎ
РэгЩЃКЩшAMЃНyЃЌдђBEЃНEMЃНxЃЌMDЃН1ЉyЃЌ
дкRtЁїAEMжаЃЌгЩЙДЙЩЖЈРэЕУAE2+AM2ЃНEM2ЃЌ
ЁрЃЈ1ЉxЃЉ2+y2ЃНx2ЃЌ
НтЕУ1+y2ЃН2xЃЌ
Ёр1Љy2ЃН2ЃЈ1ЉxЃЉ
ЁпЁЯEMPЃН90ЁуЃЌЁЯAЃНЁЯDЃЌ
ЁрRtЁїAEMЁзRtЁїDMPЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
МД![]() ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУDM![]() ЃН2ЃЎ
ЃН2ЃЎ
ЁрЁїDMPЕФжмГЄВЛБфЃЌЮЊ2ЃЎ
ЃЈ4ЃЉзїFHЁЭABгкHЃЎСЌНгBMНЛEFгкOЃЌНЛFHгкKЃЎ
дђЫФБпаЮBCFHЪЧОиаЮЃЎ
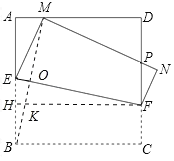
дкRtЁїAEMжаЃЌAMЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпBЁЂMЙигкEFЖдГЦЃЌ
ЁрBMЁЭEFЃЌ
ЁрЁЯKOFЃНЁЯKHBЃЌ
ЁпЁЯOKFЃНЁЯBKHЃЌ
ЁрЁЯKFOЃНЁЯKBHЃЌ
ЁпABЃНBCЃНFHЃЌЁЯAЃНЁЯFHEЃН90ЁуЃЌ
ЁрЁїABMЁеЁїHFEЃЌ
ЁрEHЃНAMЃН![]() ЃЌ
ЃЌ
ЁрCFЃНBHЃНxЉ![]() ЃЌ
ЃЌ
ЁрSЃН![]() ЃЈBE+CFЃЉBC
ЃЈBE+CFЃЉBC
ЃН![]() ЃЈx+xЉ
ЃЈx+xЉ![]() ЃЉ
ЃЉ
ЃН![]() ЃЈ2xЉ
ЃЈ2xЉ![]() ЃЉ
ЃЉ
ЃН![]() [ЃЈ
[ЃЈ![]() ЃЉ2Љ
ЃЉ2Љ![]() +1]
+1]
ЃН![]() ЃЈ
ЃЈ![]() Љ
Љ![]() ЃЉ2+
ЃЉ2+![]() ЃЎ
ЃЎ
ЁрSЃН![]() ЃЈ2xЉ
ЃЈ2xЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЕБ![]() ЃН
ЃН![]() ЪБЃЌSгазюаЁжЕЃН
ЪБЃЌSгазюаЁжЕЃН![]() ЃЎ
ЃЎ


 ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
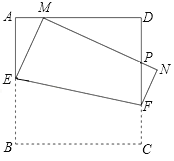
ЁОЬтФПЁПвЛеХОиаЮжНАхКЭдВаЮжНАхАДШчЭМЗНЪНЗжБ№МєЕУЭЌбљДѓЖЈРэЬиР§ЭМЃЈAC=3ЃЌBC=4ЃЌAB=5ЃЌЗжБ№вдШ§БпГЄЯђЭтМєе§ЗНаЮ) ЃЌЭМ1жаБпHIЁЂLMКЭЕуKЁЂJЖМЧЁКУдкОиаЮжНАхЕФБпЩЯЃЌЭМ2жаЕФдВаФOдкABжаЕуДІЃЌЕуHЁЂIЖМдкдВЩЯЃЌдђОиаЮКЭдВаЮжНАхЕФУцЛ§БШЪЧЃЈ ЃЉ
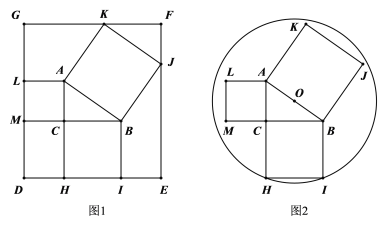
A.400:127ІаB.484:145ІаC.440:137ІаD.88:25Іа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
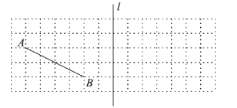
ЁОЬтФПЁПШчЭМЃЌдк![]() ЕФЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЮЊ
ЕФЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄЖМЮЊ![]() ЃЎЭјИёЯпЕФНЛЕуГЦЮЊИёЕуЃЌвдИёЕуЮЊЖЅЕуЕФШ§НЧаЮГЦЮЊИёЕуШ§НЧаЮЃЎвбжЊжБЯп
ЃЎЭјИёЯпЕФНЛЕуГЦЮЊИёЕуЃЌвдИёЕуЮЊЖЅЕуЕФШ§НЧаЮГЦЮЊИёЕуШ§НЧаЮЃЎвбжЊжБЯп![]() МАИёЕу
МАИёЕу![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧыИљОнвдЯТвЊЧѓвРДЮЛЭМЃК
ЂйдкжБЯп![]() ЕФзѓБпЛГівЛИіИёЕу
ЕФзѓБпЛГівЛИіИёЕу![]() ЃЈЕу
ЃЈЕу![]() ВЛдкжБЯп
ВЛдкжБЯп![]() ЩЯЃЉЃЌЧвТњзуИёЕу
ЩЯЃЉЃЌЧвТњзуИёЕу![]() ЪЧжБНЧШ§НЧаЮЃЛ
ЪЧжБНЧШ§НЧаЮЃЛ
ЂкЛГі![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФжсЖдГЦ
ЕФжсЖдГЦ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉТњзуЃЈ1ЃЉЕФ![]() УцЛ§ЕФзюДѓжЕЮЊЖрЩйЃП
УцЛ§ЕФзюДѓжЕЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
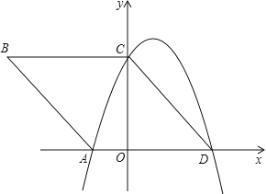
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЫФБпаЮABCDЪЧБпГЄЮЊ5ЕФСтаЮЃЌЖЅЕуAЃЎCЃЎDОљдкзјБъжсЩЯЃЌsinB=![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЙ§AЃЌCЃЌDШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉМЧжБЯпABЕФНтЮіЪНЮЊy1=mx+nЃЌЃЈ1ЃЉжаХзЮяЯпЕФНтЮіЪНЮЊy2=ax2+bx+cЃЌЧѓЕБy1>y2ЪБЃЌздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшжБЯпABгыЃЈ1ЃЉжаХзЮяЯпЕФСэвЛИіНЛЕуЮЊEЃЌPЕуЮЊХзЮяЯпЩЯAЃЌEСНЕужЎМфЕФвЛИіЖЏЕуЃЌЧвжБЯпPEНЛxжсгкЕуFЃЌЮЪЃКЕБPЕудкКЮДІЪБЃЌЁїPAEЕФУцЛ§зюДѓЃПВЂЧѓГіУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКСНжБНЧБпБШЮЊ1ЃК2ЕФжБНЧШ§НЧаЮНазіКЭКЯШ§НЧаЮЃЎ
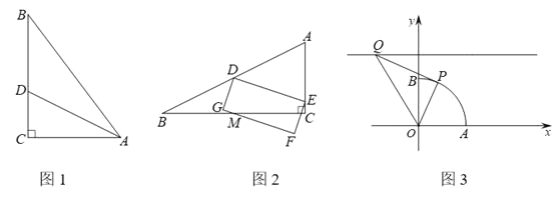
ЃЈ1ЃЉШчЭМ1ЃЌЁїABCжаЃЌЁЯC= ![]() ЃЌAC=3ЃЌBC=4ЃЌADЦНЗжЁЯCABНЛBCгкЕуDЃЌЫЕУїЁїACDЪЧКЭКЯШ§НЧаЮЃЛ
ЃЌAC=3ЃЌBC=4ЃЌADЦНЗжЁЯCABНЛBCгкЕуDЃЌЫЕУїЁїACDЪЧКЭКЯШ§НЧаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌКЭКЯЁїABCжаЃЌЁЯC= ![]() ЃЌAC=
ЃЌAC= ![]() ЃЌЕуDЪЧБпABжаЕуЃЌЕуEЪЧБпACЩЯвЛЖЏЕуЃЌдкжБЯпDEЯТЗНЙЙдьОиаЮDEFGЃЌЪЙжБЯпFGЪМжеОЙ§BCжаЕуMЃЌвбжЊЁїABCУцЛ§ЮЊ4ЃЌЧѓОиаЮDEFGЕФУцЛ§ЃЛ
ЃЌЕуDЪЧБпABжаЕуЃЌЕуEЪЧБпACЩЯвЛЖЏЕуЃЌдкжБЯпDEЯТЗНЙЙдьОиаЮDEFGЃЌЪЙжБЯпFGЪМжеОЙ§BCжаЕуMЃЌвбжЊЁїABCУцЛ§ЮЊ4ЃЌЧѓОиаЮDEFGЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЩШаЮOABжаЃЌЁЯAOB= ![]() ЃЌOA=2ЃЎвдЕуOЮЊдЕуЃЌOAЃЌOBЫљдкжБЯпЮЊзјБъжсНЈСЂЦНУцжБНЧзјБъЯЕЃЌЕуPЪЧ
ЃЌOA=2ЃЎвдЕуOЮЊдЕуЃЌOAЃЌOBЫљдкжБЯпЮЊзјБъжсНЈСЂЦНУцжБНЧзјБъЯЕЃЌЕуPЪЧ ![]() вЛЖЏЕуЃЌЕуQЪЧжБЯпy=3ЩЯвЛЖЏЕуЃЌЕБЁїOPQЪЧКЭКЯШ§НЧаЮЪБЃЌЧѓЕуPзјБъЃЎ
вЛЖЏЕуЃЌЕуQЪЧжБЯпy=3ЩЯвЛЖЏЕуЃЌЕБЁїOPQЪЧКЭКЯШ§НЧаЮЪБЃЌЧѓЕуPзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌPЪЧОиаЮ
ЃЌPЪЧОиаЮ![]() ФквЛЕуЃЌби
ФквЛЕуЃЌби![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
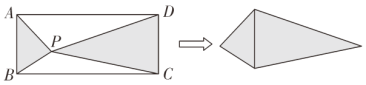
ЁЂ![]() АбетИіОиаЮМєПЊЃЌШЛКѓАбСНИівѕгАШ§НЧаЮЦДГЩвЛИіЫФБпаЮЃЌдђетИіЫФБпаЮЕФУцЛ§ЮЊ_________ЃЛетИіЫФБпаЮжмГЄЕФзюаЁжЕЮЊ________.
АбетИіОиаЮМєПЊЃЌШЛКѓАбСНИівѕгАШ§НЧаЮЦДГЩвЛИіЫФБпаЮЃЌдђетИіЫФБпаЮЕФУцЛ§ЮЊ_________ЃЛетИіЫФБпаЮжмГЄЕФзюаЁжЕЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫВтСПБЛГиЬСИєПЊЕФAЃЌBСНЕужЎМфЕФОрРыЃЌИљОнЪЕМЪЧщПіЃЌзїГіШчЭМЭМаЮЃЌЦфжаABЁЭBEЃЌEFЁЭBEЃЌAFНЛBEгкDЃЌCдкBDЩЯЃЎгаЫФЮЛЭЌбЇЗжБ№ВтСПГівдЯТЫФзщЪ§ОнЃКЂйBCЃЌЁЯACBЃЛ ЂкCDЃЌЁЯACBЃЌЁЯADBЃЛЂлEFЃЌDEЃЌBDЃЛЂмDEЃЌDCЃЌBCЃЎФмИљОнЫљВтЪ§ОнЃЌЧѓГіAЃЌBМфОрРыЕФгаЁО ЁП

AЃЎ1зщ BЃЎ2зщ CЃЎ3зщ DЃЎ4зщ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃбаОПадбЇЯАаЁзщВтСПбЇаЃЦьИЫABЕФИпЖШЃЌШчЭМдкНЬбЇТЅвЛТЅCДІВтЕУЦьИЫЖЅВПЕФбіНЧЮЊ60ЁуЃЌдкНЬбЇТЅШ§ТЅDДІВтЕУЦьИЫЖЅВПЕФбіНЧЮЊ30ЁуЃЌЦьИЫЕзВПгыНЬбЇТЅвЛТЅдкЭЌвЛЫЎЦНЯпЩЯЃЌвбжЊУПВуТЅЕФИпЖШЮЊ3УзЃЌдђЦьИЫABЕФИпЖШЮЊ
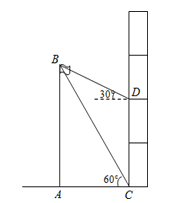
A.9УзB.6![]() УзC.6УзD.ЃЈ6+
УзC.6УзD.ЃЈ6+![]() ЃЉУз
ЃЉУз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
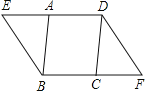
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌEЁЂFЗжБ№ЪЧDAЁЂBCбгГЄЯпЩЯЕФЕуЃЌЧвЁЯABEЃНЁЯCDFЃЎ
ЧѓжЄЃКЃЈ1ЃЉЁїABEЁеЁїCDFЃЛ
ЃЈ2ЃЉЫФБпаЮEBFDЪЧЦНааЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com