
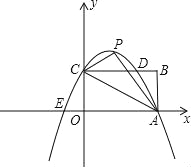
【题目】已知如图,矩形OABC的长OA=![]() ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.
(1)求∠PCB的度数;
(2)若P,A两点在抛物线y=﹣![]() x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
(3)(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
【答案】(1)∠PCB=30°.(2) ,当x=0时,y=1,故C(0,1)在抛物线的图象上.(3)M(﹣
,当x=0时,y=1,故C(0,1)在抛物线的图象上.(3)M(﹣![]() ,0),N(0,1).
,0),N(0,1).
【解析】
试题分析:(1)根据OC、OA的长,可求得∠OCA=∠ACP=60°(折叠的性质),∠BCA=∠OAC=30°,由此可判断出∠PCB的度数.
(2)过P作PQ⊥OA于Q,在Rt△PAQ中,易知PA=OA=3,而∠PAO=2∠PAC=60°,即可求出AQ、PQ的长,进而可得到点P的坐标,将P、A坐标代入抛物线的解析式中,即可得到b、c的值,从而确定抛物线的解析式,然后将C点坐标代入抛物线的解析式中进行验证即可.
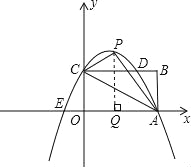
(3)根据抛物线的解析式易求得C、D、E点的坐标,然后分两种情况考虑:
①DE是平行四边形的对角线,由于CD∥x轴,且C在y轴上,若过D作直线CE的平行线,那么此直线与x轴的交点即为M点,而N点即为C点,D、E的坐标已经求得,结合平行四边形的性质即可得到点M的坐标,而C点坐标已知,即可得到N点的坐标;
②DE是平行四边形的边,由于A在x轴上,过A作DE的平行线,与y轴的交点即为N点,而M点即为A点;易求得∠DEA的度数,即可得到∠NAO的度数,已知OA的长,通过解直角三角形可求得ON的值,从而确定N点的坐标,而M点与A点重合,其坐标已知;
同理,由于C在y轴上,且CD∥x轴,过C作DE的平行线,也可找到符合条件的M、N点,解法同上.
试题解析:(1)在Rt△OAC中,OA=![]() ,OC=1,则∠OAC=30°,∠OCA=60°;
,OC=1,则∠OAC=30°,∠OCA=60°;
根据折叠的性质知:OA=AP=![]() ,∠ACO=∠ACP=60°;
,∠ACO=∠ACP=60°;
∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°.
(2)过P作PQ⊥OA于Q;
Rt△PAQ中,∠PAQ=60°,AP=![]() ;
;
∴OQ=AQ=![]() ,PQ=
,PQ=![]() ,
,
所以P(![]() ,
,![]() );
);
将P、A代入抛物线的解析式中,得: ,
,
解得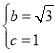 ;
;
即y=﹣![]() x2+
x2+![]() x+1;
x+1;
当x=0时,y=1,故C(0,1)在抛物线的图象上.
(3)①若DE是平行四边形的对角线,点C在y轴上,CD平行x轴,
∴过点D作DM∥CE交x轴于M,则四边形EMDC为平行四边形,
把y=1代入抛物线解析式得点D的坐标为(![]() ,1)
,1)
把y=0代入抛物线解析式得点E的坐标为(﹣![]() ,0)
,0)
∴M(![]() ,0);N点即为C点,坐标是(0,1);
,0);N点即为C点,坐标是(0,1);

②若DE是平行四边形的边,
过点A作AN∥DE交y轴于N,四边形DANE是平行四边形,
∴DE=AN=![]() =
=![]()
![]() =2,
=2,
∵tan∠EAN=![]() =
=![]() ,
,
∴∠EAN=30°,
∵∠DEA=∠EAN,
∴∠DEA=30°,
∴M(![]() ,0),N(0,﹣1);
,0),N(0,﹣1);
同理过点C作CM∥DE交y轴于N,四边形CMDE是平行四边形,
∴M(﹣![]() ,0),N(0,1).
,0),N(0,1).


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “367人中必有2人的生日是同一天”是必然事件
B. 了解一批灯泡的使用寿命采用全面调查
C. 一组数据6,5,3,5,4的众数是5,中位数是3
D. 一组数据10,11,12,9,8的平均数是10,方差是1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
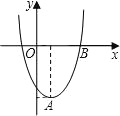
【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为( ).(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)

A.164m B.178m C.200m D.1618m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
① △ABE的面积与△BCE的面积相等;② ∠AFG=∠AGF;③ ∠FAG=2∠ACF;④ BH=CH

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com