
【题目】探究:如图①,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠B=30°,则∠ACD的度数是 度;
拓展:如图②,∠MCN=90°,射线CP在∠MCN的内部,点A、B分别在CM、CN上,分别过点A、B作AD⊥CP、BE⊥CP,垂足分别为D、E,若∠CBE=70°,求∠CAD的度数;
应用:如图③,点A、B分别在∠MCN的边CM、CN上,射线CP在∠MCN的内部,点D、E在射线CP上,连接AD、BE,若∠ADP=∠BEP=60°,则∠CAD+∠CBE+∠ACB= 度.

【答案】探究:30;(2)拓展:20°;(3)应用:120
【解析】
(1)利用直角三角形的性质依次求出∠A,∠ACD即可;
(2)利用直角三角形的性质直接计算得出即可;
(3)利用三角形的外角的性质得出结论,直接转化即可得出结论.
(1)在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°﹣∠A=30°;
故答案为:30,
(2)∵BE⊥CP,
∴∠BEC=90°,
∵∠CBE=70°,
∴∠BCE=90°﹣∠CBE=20°,
∵∠ACB=90°,
∴∠ACD=90°﹣∠BCE=70°,
∵AD⊥CP,
∴∠CAD=90°﹣∠ACD=20°;
(3)∵∠ADP是△ACD的外角,
∴∠ADP=∠ACD+∠CAD=60°,
同理,∠BEP=∠BCE+∠CBE=60°,
∴∠CAD+∠CBE+∠ACB=∠CAD+∠CBE+∠ACD+∠BCE=(∠CAD+∠ACD)+(∠CBE+∠BCE)=120°,
故答案为120.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=![]() CD,下列结论中正确的个数为( )
CD,下列结论中正确的个数为( )
①∠BAE=30°;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(2,0),以线段OA为边在第四象限内作等边三角形△AOB,点C为x正半轴上一动点(OC>2),连接BC,以线段BC为边在第四象限内作等边三角形△CBD连接DA并延长交y轴于点E.

(1)在点C的运动过程中,△OBC和△ABD全等吗?请说明理由;
(2)在点C的运动过程中,∠CAD的度数是否会变化?如果不变,请求出∠CAD的度数;如果变化请说明理由;
(3)探究当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽查部分学生做了一次问卷调查,要求学生选出自己最喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:

请根据图中信息,解答下列问题:
![]() 该调查的样本容量为______,
该调查的样本容量为______,![]() ______
______![]() ,“第一版”对应扇形的圆心角为______
,“第一版”对应扇形的圆心角为______![]() ;
;
![]() 请你补全条形统计图;
请你补全条形统计图;
![]() 若该校有1000名学生,请你估计全校学生中最喜欢“第三版”的人数.
若该校有1000名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,判断△DEF是否为等腰直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,作斜边AB上中线CD,得到第1个三角形ACD;
,作斜边AB上中线CD,得到第1个三角形ACD;![]() 于点E,作
于点E,作![]() 斜边DB上中线EF,得到第2个三角形DEF;依次作下去
斜边DB上中线EF,得到第2个三角形DEF;依次作下去![]() 则第1个三角形的面积等于______,第n个三角形的面积等于______.
则第1个三角形的面积等于______,第n个三角形的面积等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
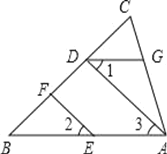
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
∵EF∥AD,(________)
∴∠2=______.(两直线平行,同位角相等;)
又∵∠1=∠2,(________)
∴∠1=∠3.(________)
∴AB∥DG.(________)
∴∠BAC+______=180°(________)
又∵∠BAC=70°,(________)
∴∠AGD=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com