
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
(1)求圆形区域的面积;
(2)某时刻海面上出现-渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离.( ≈1.7,保留三个有效数字);
≈1.7,保留三个有效数字);
(3)当渔船A由(2)中位置向正西方向航行时,是否会进入海洋生物保护区?通过计算回答。

(1)25π;(2)16.2;(3)A船不会进入海洋生物保护区.
【解析】
试题分析:(1)连接CB,CO,则CB∥y轴,由圆周角定理、勾股定理得OC=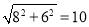 ,则半径OO′=5,S⊙O′=π•52=25π.
,则半径OO′=5,S⊙O′=π•52=25π.
(2)过点A作AD⊥x轴于点D,依题意,得∠BAD=30°,在Rt△ABD中,设BD=x,则AB=2x,由勾股定理AD= x,根据图形得到OD=OB+BD=6+x,故AB=2x=6(
x,根据图形得到OD=OB+BD=6+x,故AB=2x=6( +1)≈16.2
+1)≈16.2
(3)过点A作AG⊥y轴于点G.过点O′作O′E⊥OB于点E,并延长EO′交AG于点F.由垂径定理得,OE=BE=3.在Rt△OO′E中,由勾股定理得,O′E=4.所以O′F=9+3 -4=5+3
-4=5+3 >5.
>5.
(1)连接CB,CO,则CB∥y轴,
∴∠CBO=90°,
设O′为由O、B、C三点所确定圆的圆心.
则OC为⊙O′的直径.
由已知得OB=6,CB=8,由勾股定理得OC=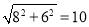
半径OO′=5,S⊙O′=π•52=25π.
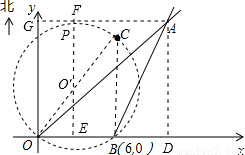
(2)过点A作AD⊥x轴于点D,依题意,得∠BAD=30°,
在Rt△ABD中,设BD=x,则AB=2x,
由勾股定理得,AD=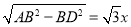 ,
,
由题意知:OD=OB+BD=6+x,在Rt△AOD中,OD=AD,6+x= x
x
∴x=3( +1),
+1),
∴AB=2x=6( +1)≈16.2
+1)≈16.2
(3)过点A作AG⊥y轴于点G.
过点O′作O′E⊥OB于点E,并延长EO′交AG于点F.
由(1)知,OO′=5,由垂径定理得,OE=BE=3.
∴在Rt△OO′E中,由勾股定理得,O′E=4
∵四边形FEDA为矩形.
∴EF=DA,而AD= x=9+3
x=9+3
∴O′F=9+3 -4=5+3
-4=5+3 >5,
>5,
∴直线AG与⊙O′相离,A船不会进入海洋生物保护区.
考点: 1.勾股定理的应用;2.点与圆的位置关系.


科目:初中数学 来源:2013-2014学年江苏省无锡市锡山区九年级下学期期中考试(一模)数学试卷(解析版) 题型:选择题
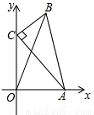
如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动.在运动过程中,点B到原点的最大距离是( )
A.6 B.2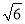 C.2
C.2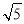 D.2
D.2 +2
+2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:解答题
如图,在△ABC中,∠BAC=90°, BC∥x轴,抛物线y=ax2-2ax+3经过△ABC的三个顶点,并且与x轴交于点D、E,点A为抛物线的顶点.

(1)求抛物线的解析式;
(2)连接CD,在抛物线的对称轴上是否存在一点P使△PCD为直角三角形,若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:选择题
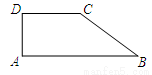
如图,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=8,CD=4,DA=3,则sinB的值是( )
A.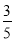 B.
B.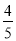 C.
C.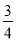 D.
D.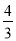
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:填空题
一台计算机硬盘容量大小是20180000000字节,请用科学记数法将该硬盘容量表示 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:解答题
演讲答辩由7位评委老师打分,民主测评由50名学生代表一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及50位同学民主测评票数统计图.

(1)求小明演讲答辩所得分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
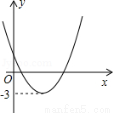
A.k<-3 B.k>-3 C.k<3 D.k>3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com