
如图,在△ABC中,∠BAC=90°, BC∥x轴,抛物线y=ax2-2ax+3经过△ABC的三个顶点,并且与x轴交于点D、E,点A为抛物线的顶点.

(1)求抛物线的解析式;
(2)连接CD,在抛物线的对称轴上是否存在一点P使△PCD为直角三角形,若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)y=-x2+2x+3;(2)P1(1,4) P2(1,-2) 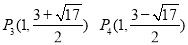 .
.
【解析】
试题分析:(1)根据题意知点B的坐标为(0,3)抛物线的对称轴方程为x=1,所以A点坐标为(1,4),C点坐标为(2,3),由此可求抛物线的解析式.
(2)分两种情况:CD为直角边,CD为斜边进行讨论,由勾股定理得到方程即可求出P点坐标.
试题解析:(1)∵y=ax2-2ax+3
∴它的对称轴为直线x=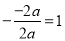
令x=0,则y=3,
∴B(0,3)
根据抛物线的对称性知:C(2,3),A(1,4)
把A(1,4)代入y=ax2-2ax+3,得:a=-1
∴抛物线的解析式为:y=-x2+2x+3;
(2)存在.分两种情况:
(1)当CD为直角边时,设P(1,a):
i)当点P在x轴上方时,DP=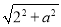 ,CP=
,CP=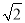 ,
,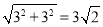 ,
,
∵CD2+CA2=AD2
∴18+2=4+a2
即:a2=16
解得a=±4(负舍去)
∴a=4
ii)当点P在x轴下方时,CD2+DP2=CP2
∴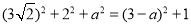
解得:a=-2
(2)当CD为斜边时,同理可以得出:a=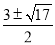
综上所述,点P的坐标分别为:P1(1,4) P2(1,-2) 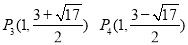
考点:二次函数综合题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源:2013-2014学年江苏省无锡市锡北片九年级4月中考模拟数学试卷(解析版) 题型:解答题
等腰△ABC中,AB=AC,边AB绕点A逆时针旋转角度m得到线段AD.
(1)如图1,若∠BAC=30°,30°<m<180°,连接BD,请用含m的式子表示∠DBC的度数;
(2)如图2,若∠BAC=60°,0°<m<360°,连接BD,DC,直接写出△BDC为等腰三角形时m所有可能的取值___ __;
(3)如图3,若∠BAC=90°,射线AD与直线BC相交于点E,是否存在旋转角度m,使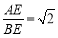 ,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市锡北片九年级4月中考模拟数学试卷(解析版) 题型:选择题
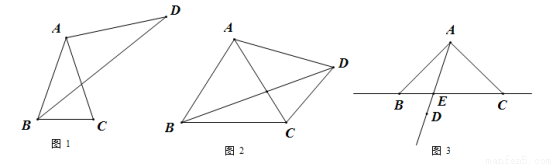
一次函数y=ax+b(a>0)、二次函数y=ax +bx和反比例函数
+bx和反比例函数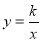 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
A.a >b>0 B.a>k>0 C.b=2a+k D.a=b+k

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市锡北片九年级4月中考模拟数学试卷(解析版) 题型:选择题
计算a3·a4的结果是( )
A.a5 B.a7 C.a8 D.a12
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:解答题
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
(1)求圆形区域的面积;
(2)某时刻海面上出现-渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离.( ≈1.7,保留三个有效数字);
≈1.7,保留三个有效数字);
(3)当渔船A由(2)中位置向正西方向航行时,是否会进入海洋生物保护区?通过计算回答。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com