【题目】已知在数轴l上，一动点Q从原点O出发，沿直线l以每秒钟2个单位长度的速度来回移动，其移动方式是先向右移动1个单位长度，再向左移动2个单位长度，又向右移动3个单位长度，再向左移动4个单位长度，又向右移动5个单位长度…
（1）求出5秒钟后动点Q所处的位置；
（2）如果在数轴l上还有一个定点A，且A与原点O相距20个单位长度，问：动点Q从原点出发，可能与点A重合吗？若能，则第一次与点A重合需多长时间？若不能，请说明理由．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】用铝片做听装饮料瓶，现有1OO张铝片，每张铝片可制瓶身16个或制瓶底45个，一个瓶身和两个瓶底可配成一套．设用x张铝片制瓶身，则下面所列方程正确的是( )
A. 2×16x= 45(100-x) B. 16x=45(100-x) C. 16x=2×45(100-x) D. 16x=45(50-x)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面说法错误的是 ( )
A. 三角形的三条角平分线交于一点 B. 三角形的三条中线交于一点
C. 三角形的三条高交于一点 D. 三角形的三条高所在的直线交于一点
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】准备一张矩形纸片，按如图操作：将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．
（1）、求证：四边形BFDE是平行四边形；
（2）、若四边形BFDE是菱形， AB＝2，求菱形BFDE的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价－进价）
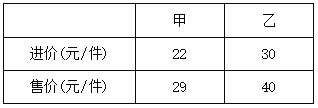
（1）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
（2）该超市第二次以第一次的进价又购进甲、乙两种商品．其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售．第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙种商品是按原价打几折销售？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE和射线AF交于点G．
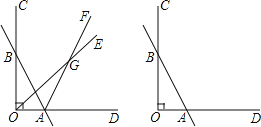
（1）若OE平分∠BOA，AF平分∠BAD，∠OBA=30°，则∠OGA=
（2）若∠GOA=
∠BOA，∠GAD=∠BAD，∠OBA=30°，则∠OGA=
（3）将（2）中“∠OBA=30°”改为“∠OBA=α”，其余条件不变，则∠OGA= α （用含α的代数式表示）
（4）若OE将∠BOA分成1：2两部分，AF平分∠BAD，∠ABO=α（30°＜α＜90°），求∠OGA的度数（用含α的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】等腰Rt△ABC中，∠BAC＝90°，AB＝AC,点A、点B分别是y轴、x轴上两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E；
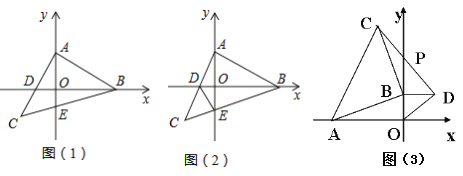
（1）如图（1），已知C点的横坐标为-1，直接写出点A的坐标；
（2）如图（2）， 当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；
（3）如图（3）， 若点A在x轴上，且A（-4，0），点B在y轴的正半轴上运动时，分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连结CD交y轴于点P,问当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由，若不变化，请求出BP的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
