
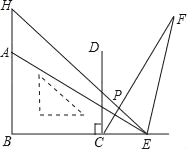
【题目】如图,点A、C分别在一个含45°的直角三角板HBE的两条直角边BH和BE上,且BA=BC,过点C作BE的垂线CD,过E点作EF⊥AE交∠DCE的角平分线于F点,交HE于P.
(1)试判断△PCE的形状,并请说明理由;
(2)若∠HAE=120°,AB=3,求EF的长.
【答案】(1)△PCE是等腰直角三角形(2)6
【解析】
(1)根据∠PCE=![]() ∠DCE=
∠DCE=![]() ×90°=45°,求证∠CPE=90°,然后即可判断三角形的形状.
×90°=45°,求证∠CPE=90°,然后即可判断三角形的形状.
(2)根据∠HEB=∠H=45°得HB=BE,再根据BA=BC和∠HAE=120°,利用ASA求证△HAE≌△CEF,得AE=EF,又因为AE=2AB.然后即可求得EF.
(1)△PCE是等腰直角三角形,
理由如下:
∵∠PCE=![]() ∠DCE=
∠DCE=![]() ×90°=45°
×90°=45°
∠PEC=45°
∴∠PCE=∠PEC
∠CPE=90°
∴△PCE是等腰直角三角形
(2)∵∠HEB=∠H=45°
∴HB=BE
∵BA=BC
∴AH=CE
而∠HAE=120°
∴∠BAE=60°,∠AEB=30°
又∵∠AEF=90°
∴∠CEF=120°=∠HAE
而∠H=∠FCE=45°
∴△HAE≌△CEF(ASA)
∴AE=EF
又∵AE=2AB=2×3=6
∴EF=6


科目:初中数学 来源: 题型:
【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.

A. 1080 B. 900 C. 600 D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地推进太原市生活垃圾分类工作,改善城市生态环境,2019年12月17日,太原市政府召开了太原市生活垃圾分类推进会,意味着太原垃圾分类战役的全面打响.某小区准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该小区物业计划用不多于2100元的资金购买A、B两种型号的垃圾箱共20个,则该小区最多可以购买B型垃圾箱多少个?
(3)在(2)的条件下,要求至少购买3个B型垃圾箱,请设计出最省钱的购买方案,并求出最少购买费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.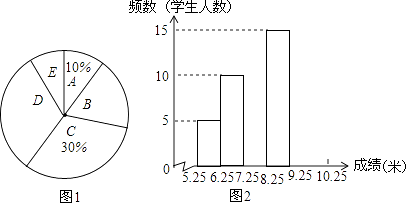
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,﹣1),E(﹣1,﹣7).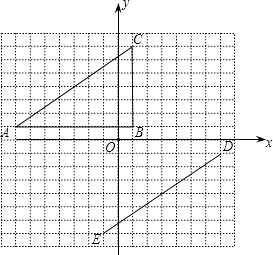
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com