
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Ν–≤ΡΝœΘ§Άξ≥…œύ”ΠΒΡ»ΈΈώΘΚ
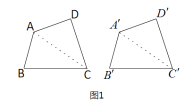
»ΪΒ»ΥΡ±Ώ–ΈΗυΨί»ΪΒ»ΆΦ–ΈΒΡΕ®“εΩ…÷ΣΘΚΥΡΧθ±ΏΖ÷±πœύΒ»Θ§ΥΡΗωΫ«“≤Ζ÷±πœύΒ»ΒΡΝΫΗωΥΡ±Ώ–Έ»ΪΒ».‘ΎΓΑΧΫΥς»ΐΫ«–Έ»ΪΒ»ΒΡΧθΦΰΓ± ±Θ§Έ“Ο«Α―ΝΫΗω»ΐΫ«–Έ÷–ΓΑ“ΜΧθ±ΏœύȖ ΜρΓΑ“ΜΗωΫ«œύȖ≥ΤΈΣ“ΜΗωΧθΦΰ.÷«Μέ–ΓΉιΒΡΆ§―ßάύ±»ΓΑΧΫΥς»ΐΫ«–Έ»ΪΒ»ΧθΦΰΓ±ΒΡΖΫΖ®Θ§ΧΫΥςΓΑΥΡ±Ώ–Έ»ΪΒ»ΒΡΧθΦΰΓ±Θ§Ϋχ––ΝΥ»γœ¬ΥΦΩΦΘΚ»γΆΦ 1Θ§ΥΡ±Ώ–ΈABCDΚΆΥΡ±Ώ–ΈA'B'C'D'÷–Θ§Ν§Ϋ”Ε‘Ϋ«œΏACΘ§A'C'Θ§’β―υΝΫΗωΥΡ±Ώ–Έ»ΪΒ»ΒΡΈ ΧβΨΆΉΣΜ·ΈΣΓΑΓςABCΓ’ΓςA'B'C'Γ±”κΓΑΓςACD Γ’ ΓςA 'C 'D 'Γ±ΒΡΈ Χβ.»τœ»ΗχΕ®ΓΑΓςABCΓ’ΓςA'B'C'Γ±ΒΡΧθΦΰΘ§÷Μ“Σ‘Ό‘ωΦ”2ΗωΧθΦΰ ΙΓΑΓςACDΓ’ΓςA'C'D'Γ±Φ¥Ω…ΆΤ≥ωΝΫΗωΥΡ±Ώ–Έ÷–ΓΑΥΡΧθ±ΏΖ÷±πœύΒ»Θ§ΥΡΗωΫ«“≤Ζ÷±πœύ»ñȧ¥”ΕχΥΒΟςΝΫΗωΥΡ±Ώ–Έ»ΪΒ».
Α¥’’÷«Μέ–ΓΉιΒΡΥΦ¬ΖΘ§–ΓΟςΕ‘ΆΦ1÷–ΒΡΥΡ±Ώ–ΈABCDΚΆΥΡ±Ώ–ΈA'B'C'D'œ»Ηχ≥ω»γœ¬ΧθΦΰΘΚABΘΫA'B'Θ§ΓœBΘΫΓœB'Θ§BCΘΫB'C'Θ§–ΓΝΝ‘Ύ¥ΥΜυ¥Γ…œ”÷Ηχ≥ωΓΑADΘΫA'D'Θ§CDΘΫC'D'Γ±ΝΫΗωΧθΦΰΘ§ΥϊΟ«»œΈΣ¬ζΉψ’βΈεΗωΧθΦΰΡήΒΟΒΫΓΑΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'Γ±.
(1)«κΗυΨί–ΓΟςΚΆ–ΓΝΝΗχ≥ωΒΡΧθΦΰΘ§ΥΒΟςΓΑΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'Γ±ΒΡάμ”…ΘΜ
(2)«κ¥”œ¬ΟφAΘ§BΝΫΧβ÷–»Έ―Γ“ΜΧβΉς¥πΘ§Έ“―Γ‘ώ______Χβ.
A.‘Ύ≤ΡΝœ÷–ΓΑ–ΓΟςΥυΗχΧθΦΰΓ±ΒΡΜυ¥Γ…œΘ§–Γ”±”÷Ηχ≥ωΝΫΗωΧθΦΰΓΑADΘΫA'D'Θ§ΓœBCDΘΫΓœB'C'D'Γ±Θ§¬ζΉψ’βΈεΗωΧθΦΰ_______(ΧνΓΑΡήΓ±ΜρΓΑ≤ΜΡήΓ±)ΒΟΒΫΓΑΥΡ±Ώ–Έ ABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'Γ±.
B.‘Ύ≤ΡΝœ÷–ΓΑ–ΓΟςΥυΗχΧθΦΰΓ±ΒΡΜυ¥Γ…œΘ§‘ΌΧμΦ”ΝΫΗωΙΊ”Ύ‘≠ΥΡ±Ώ–ΈΒΡΧθΦΰ(“Σ«σΘΚ≤ΜΆ§”Ύ–ΓΝΝΒΡΧθΦΰ)Θ§ ΙΓΑΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'Γ±Θ§ΡψΧμΦ”ΒΡΧθΦΰ «ΘΚΔΌ___________ΘΜΔΎ__________.ΘΚ
ΓΨ¥πΑΗΓΩ(1)÷ΛΟςΦϊΫβΈωΘΜ(2)AΧβΘΚ≤ΜΡήΘΜBΧβΘΚΔΌΓœD=ΓœDΓδΘΜΔΎΓœDAC=ΓœDΓδAΓδCΓδ.
ΓΨΫβΈωΓΩ
ΗυΨί»ΪΒ»»ΐΫ«–Έ≈–Ε®Ε®άμ«σΫβΦ¥Ω….
(1)÷ΛΟςΘΚ‘ΎΓςABCΚΆΓςA'B'C'÷–Θ§
ΓΏ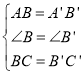
ΓύΓςABCΓ’ΓςA'B'C'(SAS)
ΓύACΘΫA'C'Θ§ΓœBACΘΫΓœB'A'C'Θ§ΓœBCAΘΫΓœB'C'A'Θ§
‘ΎΓςACD ΚΆΓςA'C'D'÷–Θ§
ΓΏ
ΓύΓςACDΓ’ΓςA'C'D'(SSS)
ΓύΓœDACΘΫΓœD'A'C'Θ§ΓœDCAΘΫΓœD'C'A'Θ§ΓœDΘΫΓœD'
ΓύΓœDAC+ΓœBACΘΫΓœD'A'C'+ΓœB'A'C'Θ§ΓœBCA+ΓœDCAΘΫΓœD'C'A'+ΓœB'C'A'
Φ¥ΘΚΓœDABΘΫΓœD'A'B'Θ§ΓœDCBΘΫΓœD'C'B'
ΓΏABΘΫA'B'Θ§BCΘΫB'C'Θ§CDΘΫC'D'Θ§DAΘΫD'A'Θ§
ΓœDABΘΫΓœD'A'B'Θ§ΓœBΘΫΓœB'Θ§ΓœDCBΘΫΓœD'C'B'Θ§ΓœDΘΫΓœD'
ΓύΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'
(2)AΧβΘΚ–ΓΟςΗχ≥ωΒΡΧθΦΰΩ…ΒΟΘΚ‘ΎΓςABCΚΆΓςA'B'C'÷–Θ§
ΓΏ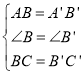
ΓύΓςABCΓ’ΓςA'B'C'(SAS)
ΓύACΘΫA'C'
ΗυΨίADΘΫA'D'Θ§ΓœBCDΘΫΓœB'C'D'Θ§≤ΜΡή≈–Ε®ΓςACDΓ’ΓςA'C'D'
Γύ≤ΜΡήΒΟΒΫΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'
Ι ¥πΑΗΈΣΘΚ≤ΜΡή
BΧβ.–ΓΟςΗχ≥ωΒΡΧθΦΰΩ…ΒΟΘΚ‘ΎΓςABCΚΆΓςA'B'C'÷–Θ§
ΓΏ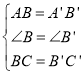
ΓύΓςABCΓ’ΓςA'B'C'(SAS)
ΓύACΘΫA'C'Θ§ΓœBACΘΫΓœB'A'C'Θ§ΓœBCAΘΫΓœB'C'A'Θ§
‘ΎΓςACDΚΆΓςA'C'D'÷–Θ§
ΓΏ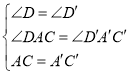
ΓύΓςACDΓ’ΓςA'C'D'(AAS)
ΓύADΘΫA'D'Θ§CDΘΫC'D'Θ§ΓœDCAΘΫΓœD'C'A'.
ΓύΓœDAC+ΓœBACΘΫΓœD'A'C'+ΓœB'A'C'Θ§ΓœBCA+ΓœDCAΘΫΓœD'C'A' +ΓœB'C'A'
Φ¥ΘΚΓœDABΘΫΓœD'A'B'Θ§ΓœDCBΘΫΓœD'C'B'
ΓΏABΘΫA'B'Θ§BCΘΫB'C'Θ§CDΘΫC'D'Θ§DAΘΫD'A'Θ§
ΓœDABΘΫΓœD'A'B'Θ§ΓœBΘΫΓœB'Θ§ΓœDCBΘΫΓœD'C'B'Θ§ΓœDΘΫΓœD'
ΓύΥΡ±Ώ–ΈABCDΓ’ΥΡ±Ώ–ΈA'B'C'D'
Ι ¥πΑΗΈΣΘΚΓœD=ΓœDΓδΘ§ΓœDAC=ΓœDΓδAΓδCΓδ.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥―ß–ΘΈΣΝΥΦ”«Ω―ΒΝΖ―ß…ζΒΡάΚ«ρΚΆΉψ«ρ‘Υ«ρΦΦΡήΘ§ΉΦ±ΗΙΚ¬ρ“Μ≈ζάΚ«ρΚΆΉψ«ρ”Ο”Ύ―ΒΝΖΘ§“―÷Σ1ΗωάΚ«ρΚΆ2ΗωΉψ«ρΙ≤–η116‘ΣΘΜ2ΗωάΚ«ρΚΆ3ΗωΉψ«ρΙ≤–η204‘Σ
![]() «σΙΚ¬ρ1ΗωάΚ«ρΚΆ1ΗωΉψ«ρΗς–ηΕύ…Ό‘ΣΘΩ
«σΙΚ¬ρ1ΗωάΚ«ρΚΆ1ΗωΉψ«ρΗς–ηΕύ…Ό‘ΣΘΩ
![]() »τ―ß–ΘΉΦ±ΗΙΚΫχάΚ«ρΚΆΉψ«ρΙ≤40ΗωΘ§≤Δ«“ΉήΖ―”Ο≤Μ≥§Ιΐ1800‘ΣΘ§‘ράΚ«ρΉνΕύΩ…ΙΚ¬ρΕύ…ΌΗωΘΩ
»τ―ß–ΘΉΦ±ΗΙΚΫχάΚ«ρΚΆΉψ«ρΙ≤40ΗωΘ§≤Δ«“ΉήΖ―”Ο≤Μ≥§Ιΐ1800‘ΣΘ§‘ράΚ«ρΉνΕύΩ…ΙΚ¬ρΕύ…ΌΗωΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥΡ¥®―≈Α≤ΖΔ…ζΒΊ’πΚσΘ§Ρ≥–Θ―ß…ζΜαœρ»Ϊ–Θ1900Οϊ―ß…ζΖΔΤπΝΥΓΑ–ΡœΒ―≈Α≤Γ±ΨηΩνΜνΕ·Θ§ΈΣΝΥΫβΨηΩν«ιΩωΘ§―ßΜα…ζΥφΜζΒς≤ιΝΥ≤ΩΖ÷―ß…ζΒΡΨηΩνΫπΕνΘ§≤Δ”ΟΒΟΒΫΒΡ ΐΨίΜφ÷ΤΝΥ»γœ¬Ά≥ΦΤΆΦΔΌΚΆΆΦΔΎΘ§«κΗυΨίœύΙΊ–≈œΔΘ§Ϋβ¥πœ¬Ν– «Έ ΧβΘΚ

Θ®1Θ©±Ψ¥ΈΫ” ήΥφΜζ≥ι―υΒς≤ιΒΡ―ß…ζ»Υ ΐΈΣΓΓΓΓΓΓΓΓΘ§ΆΦΔΌ÷–mΒΡ÷Β «ΓΓΓΓΓΓΓΓΘΜ
Θ®2Θ©«σ±Ψ¥ΈΒς≤ιΜώ»ΓΒΡ―υ±Ψ ΐΨίΒΡΤΫΨυ ΐΓΔ÷Ύ ΐΚΆ÷–ΈΜ ΐΘΜ
Θ®3Θ©ΗυΨί―υ±Ψ ΐΨίΘ§ΙάΦΤΗΟ–Θ±Ψ¥ΈΜνΕ·ΨηΩνΫπΕνΈΣ10‘ΣΒΡ―ß…ζ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐy=ax2+bx+cΘ®aΓΌ0Θ©ΒΡ≤ΩΖ÷ΆΦœσ»γΆΦΥυ ΨΘ§ΆΦœσΙΐΒψΘ®©¹1Θ§0Θ©Θ§Ε‘≥Τ÷αΈΣ÷±œΏx=2Θ§œ¬Ν–Ϋα¬έΘΚΘ®1Θ©4a+b=0ΘΜΘ®2Θ©9a+cΘΨ3bΘΜΘ®3Θ©8a+7b+2cΘΨ0ΘΜΘ®4Θ©»τΒψAΘ®©¹3Θ§y1Θ©ΓΔΒψBΘ®©¹![]() Θ§y2Θ©ΓΔΒψCΘ®
Θ§y2Θ©ΓΔΒψCΘ®![]() Θ§y3Θ©‘ΎΗΟΚ· ΐΆΦœσ…œΘ§‘ρy1ΘΦy3ΘΦy2ΘΜΘ®5Θ©»τΖΫ≥ΧaΘ®x+1Θ©Θ®x©¹5Θ©=©¹3ΒΡΝΫΗυΈΣx1ΚΆx2Θ§«“x1ΘΦx2Θ§‘ρx1ΘΦ©¹1ΘΦ5ΘΦx2Θ°Τδ÷–’ΐ»ΖΒΡΫα¬έ”–Θ®ΓΓΓΓΘ©
Θ§y3Θ©‘ΎΗΟΚ· ΐΆΦœσ…œΘ§‘ρy1ΘΦy3ΘΦy2ΘΜΘ®5Θ©»τΖΫ≥ΧaΘ®x+1Θ©Θ®x©¹5Θ©=©¹3ΒΡΝΫΗυΈΣx1ΚΆx2Θ§«“x1ΘΦx2Θ§‘ρx1ΘΦ©¹1ΘΦ5ΘΦx2Θ°Τδ÷–’ΐ»ΖΒΡΫα¬έ”–Θ®ΓΓΓΓΘ©

A. 2Ηω B. 3Ηω C. 4Ηω D. 5Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΙΛ≥ßœ÷‘ΎΤΫΨυΟΩΧλ±»‘≠ΦΤΜ°Εύ…ζ≤ζ 50 Χ®ΜζΤςΘ§œ÷‘Ύ…ζ≤ζ 600 Χ®ΜζΤςΥυ–η ±Φδ”κ‘≠ΦΤΜ°…ζ≤ζ 450 Χ®ΜζΤςΥυ–η ±ΦδœύΆ§Θ°
Θ®1Θ©œ÷‘ΎΤΫΨυΟΩΧλ…ζ≤ζΕύ…ΌΧ®ΜζΤςΘΜ
Θ®2Θ©…ζ≤ζ 3000 Χ®ΜζΤςΘ§œ÷‘Ύ±»‘≠ΦΤΜ°Χα«ΑΦΗΧλΆξ≥…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§Εΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσΒΡΕ‘≥Τ÷α «÷±œΏx=1Θ§«“Ψ≠ΙΐΒψΘ®0,2Θ©Θ°”–œ¬Ν–Ϋα¬έΘΚΔΌacΘΨ0ΘΜΔΎ
ΒΡΆΦœσΒΡΕ‘≥Τ÷α «÷±œΏx=1Θ§«“Ψ≠ΙΐΒψΘ®0,2Θ©Θ°”–œ¬Ν–Ϋα¬έΘΚΔΌacΘΨ0ΘΜΔΎ![]() ΘΜΔέa+cΘΦ2-bΘΜΔή
ΘΜΔέa+cΘΦ2-bΘΜΔή![]() ΘΜ Δίx=-5ΚΆx=7 ±Κ· ΐ÷ΒœύΒ»Θ°Τδ÷–’ΐ»ΖΒΡΫα¬έ”– Θ® Θ©
ΘΜ Δίx=-5ΚΆx=7 ±Κ· ΐ÷ΒœύΒ»Θ°Τδ÷–’ΐ»ΖΒΡΫα¬έ”– Θ® Θ©

A. 1Ηω B. 2Ηω C. 3Ηω D. 4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ Χβ«ιΨ≥ΘΚ‘ΎΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈABC÷–Θ§![]() Θ§ ÷±œΏ
Θ§ ÷±œΏ![]() ΙΐΒψ
ΙΐΒψ![]() «“
«“![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() ΈΣ“Μ»ώΫ«ΕΞΒψΉς
ΈΣ“Μ»ώΫ«ΕΞΒψΉς![]() Θ§«“Βψ
Θ§«“Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ®≤Μ”κΒψ
…œΘ®≤Μ”κΒψ![]() ÷ΊΚœΘ©Θ§»γΆΦ1Θ§
÷ΊΚœΘ©Θ§»γΆΦ1Θ§ ![]() ”κ
”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§ ‘≈–Εœ
Θ§ ‘≈–Εœ![]() ”κ
”κ![]() ΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°ΧΫΨΩ’Ι ΨΘΚ–Γ–«Ά§―ß’Ι Ψ≥ω»γœ¬’ΐ»ΖΒΡΫβΖ®ΘΚ
ΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°ΧΫΨΩ’Ι ΨΘΚ–Γ–«Ά§―ß’Ι Ψ≥ω»γœ¬’ΐ»ΖΒΡΫβΖ®ΘΚ
ΫβΘΚ![]() Θ§÷ΛΟς»γœ¬ΘΚ
Θ§÷ΛΟς»γœ¬ΘΚ
ΙΐΒψ![]() Ής
Ής![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]()
‘ρ![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ![]()
![]()
![]() Θ®“άΨί
Θ®“άΨί![]() Θ©
Θ©
‘Ύ![]() ”κ
”κ![]() ÷–
÷–
![]()
![]() Θ®“άΨί
Θ®“άΨί![]() Θ©
Θ©

Θ®1Θ©Ζ¥ΥΦΫΜΝςΘΚ…œ ω÷ΛΟςΙΐ≥Χ÷–ΒΡΓΑ“άΨί![]() Γ±ΚΆΓΑ“άΨί
Γ±ΚΆΓΑ“άΨί![]() Γ±Ζ÷±π «÷ΗΘΚ
Γ±Ζ÷±π «÷ΗΘΚ
“άΨί![]() ΘΚ
ΘΚ
“άΨί![]() ΘΚ
ΘΚ
ΆΊ’Ι―”…λΘΚΘ®2Θ©‘ΎΆΦ2÷–Θ§![]() ”κ
”κ![]() ―”≥ΛœΏΫΜ”ΎΒψ
―”≥ΛœΏΫΜ”ΎΒψ![]() Θ§ ‘≈–Εœ
Θ§ ‘≈–Εœ![]() ”κ
”κ![]() ΒΡ ΐΝΩΙΊœΒΘ§≤Δ–¥≥ω÷ΛΟςΙΐ≥Χ
ΒΡ ΐΝΩΙΊœΒΘ§≤Δ–¥≥ω÷ΛΟςΙΐ≥Χ
Θ®3Θ©‘ΎΆΦ3÷–Θ§![]() ”κ
”κ![]() ―”≥ΛœΏΫΜ”ΎΒψ
―”≥ΛœΏΫΜ”ΎΒψ![]() Θ§ ‘≈–Εœ
Θ§ ‘≈–Εœ![]() ”κ
”κ![]() ΒΡ ΐΝΩΙΊœΒΘ§≤Δ–¥≥ω÷ΛΟςΙΐ≥ΧΘ°
ΒΡ ΐΝΩΙΊœΒΘ§≤Δ–¥≥ω÷ΛΟςΙΐ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ°
Θ°
Θ®![]() Θ©
Θ©![]() Ζ÷±π»Γ
Ζ÷±π»Γ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() ±Θ§ ‘«σ≥ωΗςΚ· ΐ±μ¥ο ΫΘ§≤ΔΥΒ≥ω’β»ΐΗωΚ· ΐΒΡ“ΜΗωΙ≤Ά§ΒψΘ°
±Θ§ ‘«σ≥ωΗςΚ· ΐ±μ¥ο ΫΘ§≤ΔΥΒ≥ω’β»ΐΗωΚ· ΐΒΡ“ΜΗωΙ≤Ά§ΒψΘ°
Θ®![]() Θ©Ε‘”Ύ»Έ“βΗΚ Β ΐ
Θ©Ε‘”Ύ»Έ“βΗΚ Β ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§ ![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ‘ω¥σΘ§ ‘«σ≥ω
ΒΡ‘ω¥σΕχ‘ω¥σΘ§ ‘«σ≥ω![]() ΒΡΉν¥σ’ϊ ΐ÷ΒΘ°
ΒΡΉν¥σ’ϊ ΐ÷ΒΘ°
Θ®![]() Θ©Βψ
Θ©Βψ![]() Θ§
Θ§ ![]() «Κ· ΐΆΦœσ…œΝΫΗωΒψΘ§¬ζΉψ»τ
«Κ· ΐΆΦœσ…œΝΫΗωΒψΘ§¬ζΉψ»τ![]() Θ§ ‘±»Ϋœ
Θ§ ‘±»Ϋœ![]() ΚΆ
ΚΆ![]() ΒΡ¥σ–ΓΙΊœΒΘ°
ΒΡ¥σ–ΓΙΊœΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com